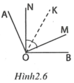
Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia OM và ON sao cho A O M ^ = B O N ^ = m ° ( 90 < m < 180 ) . Vẽ tia phân giác OC của góc MON.
a) Chứng tỏ rằng O C ⊥ A B .
b) Xác định giá trị của m để O M ⊥ O N .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Rightarrow\widehat{AOM}=\widehat{BON}\)
\(\Rightarrow\widehat{AOM}+\widehat{MOC}+\widehat{CON}+\widehat{NOB}=180^o\)
Mà: \(\widehat{AOM}=\widehat{BON},\widehat{CON}=\widehat{COM}\)
\(\Rightarrow2\widehat{AOM}+2\widehat{MOC}=180^o\)
\(\Rightarrow\widehat{AOM}+\widehat{MOC}=90^o\Leftrightarrow\widehat{AOC}=90^o\)
\(\Rightarrow CO\perp AB\)

Vì góc AOB là góc bẹt => góc AOB = 180 độ
Vì góc AOM = BON mà OC là tia phân giác của góc MON => MOC = NOC =1/2 MON
=> AOM+MOC=BON+NOC
=> AOC = BOC mà AOC+BOC= AOB
=> AOC = BOC = 180 : 2= 90 độ
=> AOC VÀ BOC là góc vuông và OC cắt AB tại O=> OC vuông góc AB

* Tìm cách giải
Để chứng tỏ O M ⊥ A B ta cần chứng tỏ góc AOM (hoặc góc BOM) có số đo bằng 90 ° .
* Trình bày lời giải
Ta có A O E ^ = B O F ^ ; M O E ^ = M O F ^ (đề bài cho)
⇒ A O E ^ + M O E ^ = B O F ^ + M O F ^ (1)
Tia OE nằm giữa hai tia OA, OM; tia OF nằm giữa hai tia OB, OM nên từ (1) suy ra A O M ^ = B O M ^ . Mặt khác, A O M ^ + B O M ^ = 180 ° (hai góc kề bù) nên A O M ^ = 180 ° : 2 = 90 ° , suy ra O M ⊥ O A . Do đó O M ⊥ A B

tia Om nằm giữa hai tia OA và OC ; tia ON nằm giữa hai tia OB và OC
do đó : \(\widehat{COA}=\widehat{O_3}+\widehat{O_1}\)và \(\widehat{COB}=\widehat{O_4}+\widehat{O_2}\)
vì \(\widehat{O_1}=\widehat{O_2}\)( gt ) ; \(\widehat{O_3}=\widehat{O_4}\)( vì tia OC là tia phân giác của \(\widehat{MON}\)) nên \(\widehat{COA}=\widehat{COB}\)
\(\widehat{COA}\)và \(\widehat{COB}\)là hai góc kề bù bằng nhau nên \(\widehat{COA}=180^o:2=90^o\)suy ra \(OC⊥AB\)

Khi đó, góc AOM+MOC+CON+NOB=180độ, AOM=BON; CON=COM nên 2.AOM+2.MOC=180độ suy ra AOM+MOC=90độ hay AOC=90độ suy ra CO vuông góc AB.
Mặt khác, tia OC là tia phân giác của góc MON nên C O N ^ = C O M ^ .
Do đó A O N ^ + C O N ^ = B O M ^ + C O M ^ (1)
Ta có tia ON nằm giữa hai tia OA, OC; tia OM nằm giữa hai tia OB, OC nên từ (1) suy ra A O C ^ = B O C ^ = 180 ° : 2 = 90 ° . Vậy O C ⊥ A B .
b) Tia OM nằm giữa hai tia OB và ON nên B O M ^ + M O N ^ = B O N ^ = m ° (1).
Mặt khác B O M ^ = 180 ° − A O M ^ = 180 ° − m ° (2).
Từ (1) và (2) suy ra: 180 ° − m ° + 90 ° = m ° ⇒ 2 m ° = 270 ° ⇒ m ° = 135 ° .
Vậy m = 135 .
Chứng minh một tia là tia phân giác, là tia đối