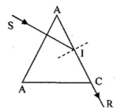
Cho tia sáng truyền tới lăng kính như hình vẽ. Tia ló truyền đi đi sát mặt BC. Chiết suất n của lăng kính có giá trị nào sau đây? (Tính tròn với 1 chữ số thập phân)
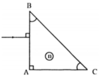
A.1,4
B.1,5
C.1,7
D. Khác A, B, C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
25 tháng 8 2018
Đáp án: C
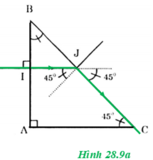
Từ hình 28.9a, ΔABC vuông cân ⇒ ∠B = ∠C = 45o
SI ⊥ AC ⇒ Tia SI truyền thẳng vào môi trường trong suốt ABC mà không bị khúc xạ ⇒ góc tới ở mặt AB bằng i1 = 0, Góc khúc xạ r1 = 0
Và góc tới mặt BC là: r2 = ∠B - r1 = 45o
Tia ló truyền sát mặt BC ⇒ góc ló i2 = 90o
→ Góc lệch tạo bởi lăng kính có giá trị: D = i1 + i2 - ∠B = 90o - 45o = 45o.
VT
1 tháng 9 2018
Đáp án: C
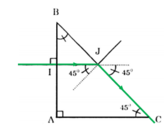
Từ hình vẽ, ΔABC vuông cân
⇒ 
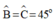
SI ⊥ AC ⇒ Tia SI truyền thẳng vào môi trường trong suốt ABC mà không bị khúc xạ ⇒ góc tới ở mặt AB bằng i 1 = 0 , Góc khúc xạ r 1 = 0
Và góc tới mặt BC là: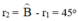 
Tia ló truyền sát mặt BC ⇒ góc ló i 2 = 90 0
→ Góc lệch tạo bởi lăng kính có giá trị:
VT
24 tháng 11 2019
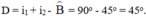
Đáp án cần chọn là: C
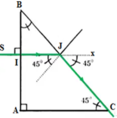
Ta có ΔABC vuông cân ⇒ B ^ = C ^ = 45 0
S I ⊥ A B ⇒ Tia SI truyền thẳng vào môi trường trong suốt ABC mà không bị khúc xạ
→ Góc tới ở mặt AB là i 1 = 0 và góc khúc xạ r 1 = 0
Tia ló truyền sát mặt BC → Góc ló i 2 = 90 0
→ Góc lệch tạo bởi lăng kính có giá trị:
D = i 1 + i 2 − B ^ = 0 + 90 0 − 45 0 = 45 0
VT
22 tháng 7 2019
Ta thấy tia ló truyền đi sát mặt BC ⇒ góc tới mặt BC bằng góc giới hạn: r2 = igh
Và sin igh = 1/n
Mà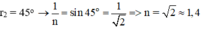 
Đáp án: A
VT
5 tháng 9 2019
Đáp án cần chọn là: A
+ Vì chiếu tia tới vuông góc với mặt AB nên i 1 = 0 ⇒ r 1 = 0
+ Ta có, góc chiết quang A = r 1 + r 2 = 0 + r 2 ⇒ A = r 2
+ Vì tia ló đi là là mặt AC nên i 2 = 90 0
Áp dụng định luật khúc xạ ánh sáng tại mặt AC, ta có:
sin i 2 = n sin r 2
⇔ sin 90 0 = 2 sinr 2
⇒ sinr 2 = 1 2 ⇒ r 2 = 45 0
=> Góc chiết quang của lăng kính A = r 2 = 45 0
Đáp án cần chọn là: A
Ta có ΔABC vuông cân ⇒ B ^ = C ^ = 45 0
S I ⊥ A B ⇒ Tia SI truyền thẳng vào môi trường trong suốt ABC mà không bị khúc xạ
→ Góc tới ở mặt AB là i 1 = 0 và góc khúc xạ r 1 = 0
Góc tới mặt BC là: r 2 = 90 0 − B J I ^ = 90 0 − 45 0 = 45 0
Tia ló truyền sát mặt BC → Góc ló i 2 = 90 0
Áp dụng định luật khúc xạ ánh sáng ta có:
n . sin r 2 = sin i 2 ⇒ n = sin i 2 sin r 2 = sin 90 sin 45 = 1,4