Một lăng kính thủy tinh có chiết suất n = 2 . Tiết diện thẳng của lăng kính là một tam giác đều ABC. Chiếu một tia sáng nằm trong mặt phẳng của tiết diện thẳng, tới AB với góc tới i 1 = 45 0 . Góc lệch D của lăng kính có giá trị là:
A. 45 0
B. 60 0
C. 30 0
D. 90 0


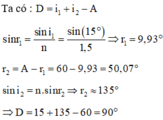
Đáp án cần chọn là: C
Áp dụng định luật khúc xạ ánh sáng tại I, ta có:
sin i 1 = n sin r
⇔ sin 45 0 = 2 sinr 1
⇒ sinr 1 = 1 2 ⇒ r 1 = 30 0
+ Lại có góc chiết quang
A = 60 0 = r 1 + r 2
⇒ r 2 = A − r 1 = 60 0 − 30 0 = 30 0
+ Áp dụng định luật khúc xạ ánh sáng tại J, ta có:
sin i 2 = n sin r 2
⇔ sin i 2 = 2 sin 30 0 = 2 2
⇒ i 2 = 45 0
+ Góc lệch của lăng kính: D = i 1 + i 2 − A = 45 0 + 45 0 − 60 0 = 30 0