Cho góc α thỏa mãn tanα = 5. Tính P= sin4 α - cos4 α
A. P = 2
B. P = 1/2
C. P = 11/13
D. P = 12/13
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 3 2018
Chọn B.
Ta có: 1 + cos2α = 2cos2α và sin2α = 2sinα.cosα.
Mà tanα = 2 nên cot α = 1/2
Suy ra:
CM
8 tháng 3 2019
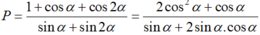
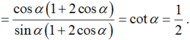
Chọn C.
Ta có tan α – cotα = 1
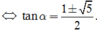
Do 
suy ra tanα < 0 nên
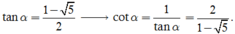
Thay
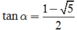và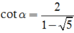 
vào P ta được
PT
1
CM
29 tháng 6 2018
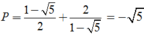
Chọn B.
Ta có P = tan3α + cot3α = (tanα + cotα) 3 - 3tanα.cotα( tanα + cotα)
= 53 - 3.5 = 110
CM
18 tháng 9 2019
Ta có:
C = sin 4 α + cos 4 α = sin 4 α + cos 4 α + 2 sin 2 α . cos 2 α - 2 sin 2 α . cos 2 α
= sin 2 α + cos 2 α 2 - 2 sin 2 α . cos 2 α
= 1 - 2 sin 2 α . cos 2 α ( v ì sin 2 α + cos 2 α = 1 )
Vậy C = 1 - 2 sin 2 α . c o s 2
Đáp án cần chọn là: A
Chọn D.
Ta có P = ( sin2α - cos2α) ( sin2α + cos2α) = sin2α - cos2α (*)
Chia hai vế của (*) cho cos2 α ta được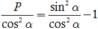
Tương đương: P(1 + tan2α) = tan2α - 1