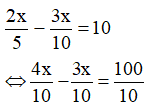Một ô tô đi từ Hà Nội đến Thanh Hoá vs V= 40km/h. Sau 2h nghỉ lại ở Thanh Hoá , ô tô lại từ Thanh Hoá về Hà Nội vs V= 30km/h. Tổng thời gian cả đi lẫn về là 10h45p. Tính quãng đường - Thanh Hoá
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 4 2022
Gọi quãng đường AB là x ( km ) ( x>0 )
Thời gian đi là \(\dfrac{x}{40}\) (h)
Thời gian về là: \(\dfrac{x}{30}\) (h)
2 giờ 15 phút = 9/4 giờ
Theo đề bài ta có pt:
\(\dfrac{x}{40}+\dfrac{x}{30}+\dfrac{9}{4}=11\)
\(\Leftrightarrow x\left(\dfrac{1}{40}+\dfrac{1}{30}\right)=\dfrac{35}{4}\)
\(\Leftrightarrow\dfrac{7}{120}x=\dfrac{35}{4}\)
\(\Leftrightarrow x=150\left(tm\right)\)
Vậy quãng đường AB dài 150 km
15 tháng 7 2021
Bài 4:
1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có BD là đường cao ứng với cạnh AC(gt)
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)
mà AD+CD=AC=8cm(D nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó: AD=3(cm)
b) Xét ΔABI và ΔCBD có
\(\widehat{ABI}=\widehat{CBD}\)(BD là tia phân giác của \(\widehat{ABC}\))
\(\widehat{IAB}=\widehat{DCB}\left(=90^0-\widehat{ABH}\right)\)
Do đó: ΔABI\(\sim\)ΔCBD(g-g)
AH
Akai Haruma
Giáo viên
28 tháng 2 2022
Lời giải:
Tổng thời gian đi lẫn về (không tính thời gian nghỉ) là:
$10h45-2=8h45=8,75h$
Thời gian đi: $\frac{AB}{40}$
Thời gian về: $\frac{AB}{30}$
$\Rightarrow \frac{AB}{40}+\frac{AB}{30}=8,75$
$\Leftrightarrow \frac{7}{120}AB=8,75$
$\Leftrightarrow AB=150$ (km)
28 tháng 2 2022
Bài 1:
Gọi độ dài quãng đường là x
Theo đề, ta có phương trình: x/40+x/30+2=10,75
=>x/40+x/30=8,75
hay x=150
28 tháng 2 2022
Tham khảo:
Bài 1:
Gọi a (km) (a > 0) là quãng đường Hà Nội - Thanh Hóa.
Thời gian lúc đi là a/40 (giờ)
Thời gian lúc về là a/30 (giờ)
Tổng thời gian đi và về không kể thời gian nghỉ ở Thanh Hóa là:
10 giờ 45 phút – 2 giờ = 8 giờ 45 phút = 8.3/4 giờ = 35/4 giờ
Theo để bài, ta có phương trình: a/40 + a/30 = 35/4
⇔ 3a/120 + 4a/120 = 1050/120 ⇔ 3a + 4a = 1050
⇔ 7a = 1050 ⇔ a = 150 (thỏa)
Vậy quãng đường Hà Nội - Thanh Hóa dài 150 km.
Bài 2:
Gọi x (km) là quãng đường Hà Nội - Hải Phòng. Điều kiện: x > 0
Thời gian dự định đi:
10 giờ 30 phút - 8 giờ = 2 giờ 30 phút = 5/2 giờ
Thời gian thực tế đi:
11 giờ 20 phút - 8 giờ = 3 giờ 20 phút = 10/3 giờ
Vận tốc dự định đi: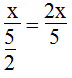
(km/h)
Vận tốc thực tế đi: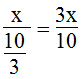 
(km/h)
Vận tốc thực tế đi chậm hơn vận tộc dự định đi 10 km/h nên ta có phương trình:
Vậy quãng đường Hà Nội - Hải Phòng dài 100km.
1 tháng 4 2016
Gọi tgian đi từ HN->TH là x(h)(0<x<10)
=>tgian đi từ TH->HN là 10-2-x=8-x(h)
Theo bài ra ta có: 40x=30.(8-x)
<=>40x=240-30x
<=>70x=240
<=>x=24/7(tm đk)
=>Độ dài quãng đường HN-TH là 40.24/7=960/7(km)
5 tháng 7 2017
Nếu ko kể thời gian nghỉ, tổng thời gian đi và về là:
10 - 2 = 8(giờ)
Tỉ số giữa vận tốc đi từ Hà Nội đến Thanh Hóa và vận tốc từ Thanh Hóa về Hà Nội là:
40 : 30 = \(\frac{4}{3}\)
Vì cùng một quãng đường thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên tỉ số của thời gian đi từ Hà Nội đến Thanh Hóa và thời gian từ Thanh Hóa về Hà Nội là \(\frac{3}{4}\)
Thời gian từ Hà Nội đến Thanh Hóa là:
\(8:\left(3+4\right).3=\frac{24}{7}\)(giờ)
Quãng đường Hà Nội-Thanh Hóa là:
\(40.\frac{24}{7}=\frac{960}{7}\)(km)
CM
19 tháng 1 2017
Gọi a (km) (a > 0) là quãng đường Hà Nội - Thanh Hóa.
Thời gian lúc đi là a/40 (giờ)
Thời gian lúc về là a/30 (giờ)
Tổng thời gian đi và về không kể thời gian nghỉ ở Thanh Hóa là:
10 giờ 45 phút – 2 giờ = 8 giờ 45 phút = 8.3/4 giờ = 35/4 giờ
Theo để bài, ta có phương trình: a/40 + a/30 = 35/4
⇔ 3a/120 + 4a/120 = 1050/120 ⇔ 3a + 4a = 1050
⇔ 7a = 1050 ⇔ a = 150 (thỏa)
Vậy quãng đường Hà Nội - Thanh Hóa dài 150 km.
TT
22 tháng 4 2021
Gọi quãng đường HN-HP là x (x>0) km
thời gian đi hết quãng đường là \(\dfrac{x}{40}\) h
thời gian về là \(\dfrac{x}{30}\) h
vì tổng thời gian cả đi và về ( tính cả thời gian nghỉ ) là 11h nên ta có pt
\(\dfrac{x}{40}\) +\(\dfrac{x}{30}\) +2.25=11
giải pt x= 150 TM
vậy quãng đường Hà Nội - Hải Phòng là 150 km
