Cho tam giác ABC vuông tại A (AB < AC), tia phân giác BM (M ∈ AC). Vẽ MK vuông góc với BC tại K. gọi N là giao điểm của MK và AB. Chứng minh:
d. BM vuông góc với NC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 11 2019
a. Hình vẽ (0.5 điểm)
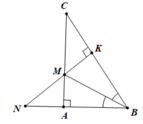
Xét ΔABM và ΔKBM có:
∠(ABM) = ∠(KBM)
BM là cạnh chung
⇒ ΔABM = ΔKBM(cạnh huyên – góc nhọn) (1 điểm)
⇒ AM = MK và BA = BK (hai cạnh tương ứng) ⇒ M, B nằm trên đường trung trực của AK (0.5 điểm)
Suy ra BM là đường trung trực của AK
CM
9 tháng 2 2017
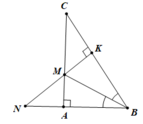
b. Xét ΔAMF và ΔKMC có:
AM = MK
∠(AMN) = ∠(KMC) (hai góc đối đỉnh)
⇒ ΔAMF = ΔKMC ( cạnh góc vuông – góc nhọn kề) (0.5 điểm)
⇒ MN = MC (hai cạnh tương ứng) (0.5 điểm)
CM
13 tháng 3 2019
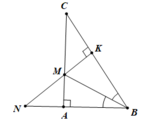
c. Do tam giác MKC vuông tại K nên MK < MC (0.5 điểm)
Mà MA = MK ⇒ MA < MC (0.5 điểm)
N
6 tháng 3 2020
Tự vẽ hình nhé ?
a) Xét ∆ABM và ∆KBM có :
Góc BAM = BKM (do AB ⊥ AC, MK ⊥ BC (GT))
BM chung
Góc ABM = KBM (do BM là tia pg của góc ABC (GT))
=> ∆ABM = ∆KBM (ch - gn) (1)
=> Góc AMB = KMB (2 góc tương ứng)
Mà MB nằm giữa MA và MK
=> MB là tia pg của góc AMK (đpcm)
b) Từ (1) => AM = KM (2 cạnh tương ứng) (2)
Ta có : Góc BAM (=90o) + NAM = 180o (kề bù)
Mà góc BKM (=90o) + CKM = 180o (kề bù)
=> Góc NAM = CKM (3)
Xét ∆ANM và ∆KCM có :
Góc AMN = CMK (đối đỉnh)
AM = KM (Theo (2))
Góc NAM = CKM (Theo (3))
=> ∆ANM = ∆KCM (g.c.g)
=> MN = MC (2 cạnh tương ứng)
Vậy...
18 tháng 6 2023
a: Xét ΔAMB vuông tại M và ΔANC vuông tại N có
AB=AC
góc A chung
=>ΔAMB=ΔANC
b: AN=căn 10^2-8^2=6cm=AM
c: Xét ΔNAH vuông tại N và ΔMAH vuông tại M có
AH chung
AN=AM
=>ΔNAH=ΔMAH
=>góc NAH=góc MAH
=>H nằm trên tia phân giác của góc BAC
6 tháng 11 2017
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.
8 tháng 3 2023
a: Xét ΔCAM vuông tại A và ΔCNM vuông tại N có
CM chung
góc ACM=góc NCM
=>ΔCAM=ΔCNM
b: Xét ΔMAK vuông tại A và ΔMNB vuông tại N có
MA=MN
góc AMK=góc NMB
=>ΔMAK=ΔMNB
=>MK=MB
12 tháng 5 2023
a: Xét ΔBHI vuông tại H và ΔAKI vuông tại K có
góc BIH=góc AIK
=>ΔBHI đồng dạng vói ΔAKI
=>IB*IK=IA*IH
b: góc BHA=góc BKA=90 độ
=>BHKA nội tiếp
=>góc BAH=góc BKH
d. Trong tam giác ANC có hai đường cao CA và NK cắt nhau tại M nên M là trực tâm tam giác ANC (0.5 điểm)
Suy ra BM cũng là đường cao của tam giác ANC
BM vuông góc với CN (0.5 điểm)