Cho tam giác ABC (AC > AB), trung tuyến AM. Trên tia đối của tia MA lấy D sao cho MD = MA
a. Chứng minh ΔMAB = ΔMDC rồi suy ra AB = CD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nãy làm xong ấn f5 mất cái hình đẹp,tức ghê,giờ không làm kỹ nữa.Bạn tự ký hiệu vô hình
a) Dễ chứng minh tam giác MAB = tam giác MDC (c.g.c)
Suy ra AB = CD (hai cạnh tương ứng)
b)*chứng minh góc ADC > góc DAC
Xét tam giác ACD,theo quan hệ giữa góc và cạnh đối diện,ta cần chứng minh AC > CD = AB
Điều này hiển nhiên đúng do giả thiết đề bài,
*chứng minh góc MAB > góc MAC
Từ kết quả câu a) suy ra góc MAB = góc MDC
Ta cần chứng minh MDC > MAC
Theo đề bài dễ có A,M,D thẳng hàng (do AM và MD là hai tia đối nhau)
Suy ra góc MDC = ADC
MAC = DAC
Từ kết quả phía trên ta suy ra góc ADC = góc MDC > góc DAC = MAC
c)*So sánh HC và HB
Do AB < AC theo quan hệ giữa hình chiếu và đường xiên suy ra HB < HC
*So sánh EB và EC
Do HB < HC nên cũng theo quan hệ giữa hình chiếu và đường xiên,suy ra EB < EC
Vậy....
P/s: Lâu không làm dạng này nên mình không chắc,nhất là câu c ấy

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD

b. Theo câu a, AB = CD mà AB < AC ⇒ CD < AC (0.5 điểm)
Trong tam giác ADC có CD < AC ⇒ ∠(DAC) < ∠(ADC) (0.5 điểm)
Mà ∠(BAM) = ∠(ADC) ( 2 góc tương ứng vì ΔABM = ΔDCM)
Suy ra (MAB) > (MAC) (0.5 điểm)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AC^2+AB^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=10^2-8^2=36\)
hay \(AC=\sqrt{36}=6cm\)
Vậy: AC=6cm

a: Xet ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
b: ΔMAB=ΔMDC
=>góc MAB=góc MDC
=>AB//CD
c: Xét tứ giác ABCE có
N là trung điểm chung của AC và BE
=>ABCE là hình bình hành
=>AB//EC
=>C,E,D thẳng hàng

a)Xét hai tam giác ABM và DMC, ta có:
MA= MD(gt)
Góc ABM=CMD(đối đỉnh)
MB=MC(Vì AM là đường trung tuyến)
=> Tam giác ABM= Tam giác DMC(c.g.c)
b)Xét hai tam giác vuông AHB và EHB, ta có
AH=EH(gt)
AH: cạnh chung
=>tam giác AHB= tam giác EHM( 2 cạnh góc vuông)
=>AB=EM( 2 cạnh tương ứng)
=>tam giác ABE cân tại B
mình chỉ biết giải 2 câu thuj

a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: ta có: ΔAMB=ΔDMC
nên AB=DC
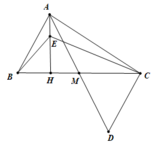
a. Hình vẽ (0.5 điểm)
Xét ΔABM và ΔDCM có:
BM = MC
∠(AMB) = ∠(BMC)
AM = MD
⇒ ΔABM = ΔDCM (c.g.c) (0.5 điểm)
⇒ AB = DC (hai cạnh tương ứng) (0.5 điểm)