Cho hàm số y = 2 x - 1 x + 1 có đồ thị là (C). Gọi I là giao điểm 2 đường tiệm cận. Gọi M x 0 , y 0 , x 0 > 0 là một điểm trên (C) sao cho tiếp tuyến với (C) tại M cắt hai đường tiệm cận lần lượt tại A, B thỏa mãn A B 2 + I B 2 = 40 . Khi đó tích x 0 y 0 bằng
A. 15 4
B. 1 2
C. 1
D. 2



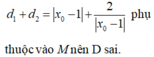

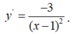
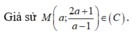
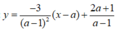
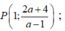
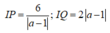
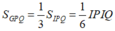
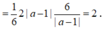
Giao điểm của hai đường tiệm cận là I ( -1;2 )
y = 2 x - 1 x + 1 ⇒ y ' = 3 x + 1 2 ⇒ PTTT tại M x 0 , y 0 là
( d ) y = 3 x 0 + 1 2 x - x 0 + 2 x 0 - 1 x 0 + 1
Giao của (d) với TCD x = -1 là A - 1 ; 2 x 0 - 4 x 0 - 1 , Giao của (d) với TCD B 2 x 0 + 1 ; 2
A B 2 + I B 2 = 40 ⇔ 2 - 2 x 0 - 4 x 0 - 1 2 + - 2 x 0 - 2 2 = 40
⇔ 36 x 0 + 1 2 + 4 x 0 + 1 2 = 40
x 0 + 1 4 - 10 x 0 + 1 2 + 9 = 0 ⇔ x 0 + 1 2 = 1 x 0 + 1 2 = 9 ⇒ x 0 = 2 x 0 > 0 ⇒ y 0 = - 1 ⇒ x 0 y 0 = 2
Đáp án cần chọn là D