Question

[Nguyễn Hồng Vũ]

Trả lời giúp mình câu hỏi này gấp nhé, gấp nhé:

Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0

a) Chứng minh rằng (α) cắt ( β)

b) Viết phương trình tham số của đường thẳng d là giao của (α) và ( β)

c) Tìm điểm M' là ảnh của M(4; 2; 1) qua phép đối xứng qua mặt phẳng (α).

d) Tìm điểm N' là ảnh của N(0; 2; 4) quá phép đối xứng qua đường thẳng d.

Answer 1

[Hồ Nhật Phi]

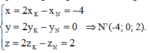
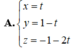
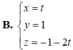
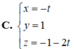
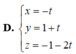
a) Vector pháp tuyến của hai mặt phẳng (\(\alpha\)) và (\(\beta\)) lần lượt là \(\overrightarrow{n_{\alpha}}\)=(4;1;2) và \(\overrightarrow{n_{\beta}}\)=(2; -2;1). Do hai vector này không cùng phương nên hai mặt phẳng (\(\alpha\)) và (\(\beta\)) cắt nhau.

b) Với x=0, \(\left\{{}\begin{matrix}y+2z+1=0\\-2y+z+3=0\end{matrix}\right.\)⇒ \(\left\{{}\begin{matrix}y=1\\z=-1\end{matrix}\right.\).

Với x=1, \(\left\{{}\begin{matrix}4+y+2z+1=0\\2-2y+z+3=0\end{matrix}\right.\)⇒ \(\left\{{}\begin{matrix}y=1\\z=-3\end{matrix}\right.\).

Suy ra đường thẳng d đi qua hai điểm A(0;1; -1) và B(1;1; -3), \(\overrightarrow{u_d}\)=\(\overrightarrow{AB}\)=(1;0;-2).

Phương trình cần tìm:

d: \(\left\{{}\begin{matrix}x=t\\y=1\\z=-1-2t\end{matrix}\right.\).

c) Gọi M'(x;y;z). Phương trình đường thẳng d' đi qua M(4;2;1) và nhận vector \(\overrightarrow{n_{\alpha}}\)=(4;1;2) làm vector chỉ phương là:

d': \(\left\{{}\begin{matrix}x=4+4t\\y=2+t\\z=1+2t\end{matrix}\right.\). Gọi M"(4+4t; 2+t; 1+2t) ∈ d'.

M"=d'\(\cap\)(α) ⇒ 4(4+4t)+2+t+2(1+2t)+1=0 ⇒ t= -1 ⇒ M''(0;1; -1).

Điểm M' đối xứng với M qua M'', suy ra M'(-4;0; -3).

d) Gọi N'(a;b;c). Phương trình mp(P) đi qua N(0;2;4) và nhận vector \(\overrightarrow{u_d}\)=(1;0; -2) làm vector pháp tuyến là:

(P): x -2z+8=0. Gọi N''(t;1; -1 -2t) ∈ d.

N''=d\(\cap\)(P) ⇒ t -2( -1 -2t)+8=0 ⇒ t= -2 ⇒ N''(-2;1;3).

Điểm N' đối xứng với N qua N'', suy ra N'(-4;0;2).