Hai ô tô cùng đi từ A đến B. Vì vậ tốc của ô tô thứ nhất bằng 60% vận tốc của ô tô thứ hai nên ô tô thứ nhất đến B chậm hơn ô tô thứ hai 2h. Thời gian ô tô thứ hai đi từ A đến B là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 8 2015
Ô tô thứ nhất kém ô tô thứ hai:
100-60=40%(ô tô thứ 2)
ô tô thứ 2 đến B hết là:
2:40%=5(h)
ô tô thứ 2 hết:
5+5.60%=8(giờ)
13 tháng 2 2016
Trên cùng quãng đường AB,vận tốc và thời gian là 2 đại lượng tỉ lệ nghịch mà vận tốc ô tô thứ 1 bằng 60% (= 3/5) vận tốc ô tô thứ 2 nên thời gian ô tô thứ 1 đi hết quãng đường AB bằng 5/3 ô tô thứ 2.
=> Ô tô thứ 2 đi từ A đến B hết : 2 : (5-3).3 = 3 (giờ)
CM
19 tháng 11 2018
Gọi v 1 ; v 2 lần lượt là vận tốc của xe thứ nhất và xe thứ hai (km/h) ( v 1 ; v 2 > 0)
Gọi t 1 ; t 2 lần lượt là thời gian của xe thứ nhấy và xe thứ hai (h) ( t 1 ; t 2 > 0)
Từ đề bài ta có: v 1 = 60 100 v 2 ⇒ v 1 = 3 5 v 2 và t 1 = t 2 + 4
Vì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên ta có:
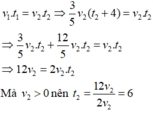
Vậy thời gian người thứ hai đi từ A đến B là 6h
Đáp án cần chọn là B
CM
24 tháng 12 2019
Gọi v 1 ; v 2 lần lượt là vận tốc của xe thứ nhất và xe thứ hai (km/h) ( v 1 ; v 2 > 0)
Gọi t 1 ; t 2 lần lượt là thời gian của xe thứ nhấy và xe thứ hai (h) ( t 1 ; t 2 > 0)
Từ đề bài ta có: v 1 = 120 100 v 2 ⇒ v 1 = 6 5 v 2 và t 2 = t 1 + 2
Vì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên ta có:
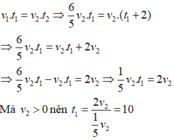
Vậy thời gian người thứ hai đi từ A đến B là t 2 = 10 + 2 = 12 h
Đáp án cần chọn là B
20 tháng 12 2015
0,6=3/5
Vì 2 ô tô cùng đi từ A đến B nên thời gian(x) tỉ lệ thuận với vận tốc (y)
nên \(\frac{x_1}{y_2}=\frac{x_2}{y_1}\) hay \(\frac{x_1}{5}=\frac{x_2}{3}\)
Ta có: x1-x2=4(giờ)
Áp dụng tính chất dãy tỉ số bằng nhau , ta được:
\(\frac{x_1}{5}=\frac{x_2}{3}=\frac{x_1-x_2}{5-3}=\frac{4}{2}=2\)
Do đó, x1=2*5=10
x2=2*3=6
Vậy thời gian 2 xe đi từ A đến B lần lượt là: 10;6(giờ)
