cho 1 số nguyên dương n(0<N<1000) dữ liệu vào cho trong tep timso.inp có duy nhất 1 số n dữ liệu ra ghi vào tệp timso.out số lượng các số có 3 chữ số thỏa mãn số đó bằng n lần tổng các bình phương các chữ số của nó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 8 2017
Đáp án B
Ta có: log a 2019 + log a 2019 + ... + log a n 2019
= log a 2019 + 2 log 2019 + ... + n log a 2019
= log a 2019 1 + 2 + ... + n = n 2 n + 1 log a 2019
= 2033136 log a 2019 ⇒ n 2 n + 1 = 2033136
⇔ n 2 + n − 4066272 = 0 ⇔ n = 2016 n = − 2017 ⇒ n = 2016.
23 tháng 12 2021
#include <bits/stdc++.h>
using namespace std;
long long n,i;
int main()
{
cin>>n;
if (n>0) cout<<"N phai la so duong";
else {
for (i=1; i<=n; i++) cout<<i<<" ";
}
return 0;
}
24 tháng 6 2015
Chứng minh tính chất: Nếu mọi số nguyên k (2 \(\le\) k \(\le\)[ \(\sqrt{N}\)] ) đều không là ước của N thì N là số nguyên tố
C/M: Giả sử N không là số nguyên tố
= N = kx1 ky2 ...kmz trong đó 2 \(\le\) k1 < k2 < ...< kn
=> N > kn1 \(\ge\)k12
=> k1 \(\le\) \(\sqrt{N}\); k nguyên => k1 \(\le\) [\(\sqrt{N}\)]
mà k1 là ước của N => Mâu thuẫn với giả thiết
Vậy N kà số nguyên tố
CM
11 tháng 4 2017
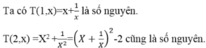
\Ta sẽ chứng minh T(1,x) là số nguyên
Thật vậy, áp dụng phép chứng minh quy nạp, Ta có:
Bước cơ sở: T(1,x) là số nguyên. Khẳng định đúng với n=1
Bước quy nạp: Giả sử T(n,x) là số nguyên với mọi n≥1. Ta sẽ chứng minh T(n+1,x) cũng là số nguyên
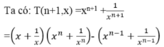
=T(1,x).T(n,x) – T(n-1,x).
Theo giả thuyết quy nạp, Ta có T(1,x),T(n,x), T(n-1,x) là các số nguyên nên T(n+1,x) là số nguyên
Chọn C
11 tháng 12 2021
1:
#include <bits/stdc++.h>
using namespace std;
long long n,i,dem,x;
int main()
{
cin>>n;
dem=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (x==0) dem++;
}
cout<<dem;
return 0;
}
