Cho hai đường thẳng cắt nhau d 1 : 3 x − 4 y + 1 = 0 v à d 2 : x + 3 = 0 . Phương trình các phân giác góc tạo bởi d1d2 là
A.x + 2y + 7 = 0 và 2x – y + 7 = 0
B.x + 2y + 4 = 0 và 2x – y + 4 = 0
C.x + 2 y + 7 = 0 và 2x – y + 4 = 0
D.x + 2y – 7 = 0 và 2x – y – 7 = 0


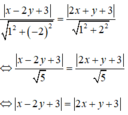
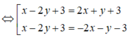
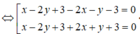
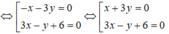
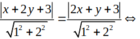
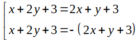
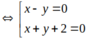



Cho 2 đường thẳng cắt nhau d 1 : a 1 x + b 1 y + c 1 = 0 v à d 2 : a 2 x + b 2 y + c 2 = 0 .
Khi đó, phương trình đường phân giác tạo bởi 2 đường thẳng là:
a 1 x + b 1 y + c 1 a 1 2 + b 1 2 = ± a 2 x + b 2 y + c 2 a 2 2 + b 2 2
Áp dụng công thức ta có phương trình hai phân giác là:
3 x − 4 y + 1 3 2 + ( − 4 ) 2 = ± x + 3 1 2 + 0 2 ⇔ 3 x − 4 y + 1 5 = ± ( x + 3 ) ⇔ 3 x − 4 y + 1 = ± 5 x + 3 ⇔ 2 x + 4 y + 14 = 0 8 x − 4 y + 16 = 0 ⇔ x + 2 y + 7 = 0 2 x − y + 4 = 0
ĐÁP ÁN C