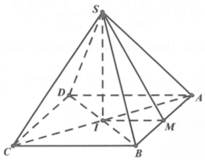
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng a 3 . Gọi V 1 , V 2 lần lượt thể tích khối cầu và khối nón ngoại tiếp hình chóp S.ABCD. Tính tỷ số V 1 V 2
A. V 1 V 2 = 324 25
B. V 1 V 2 = 18 30 25
C. V 1 V 2 = 36 25
D. V 1 V 2 = 108 25





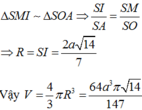
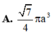
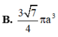
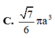
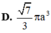


Đáp án D.
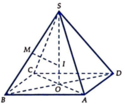
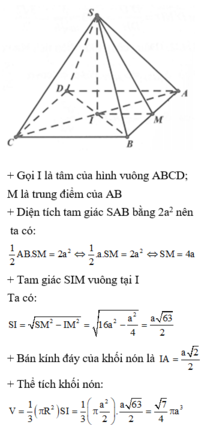
Gọi O là tâm của hình vuông ABCD.vì S.ABCD là hình chop đều nên SO ⊥ (ABCD)
Từ giả thiết, ta có
Khối nón ngoại tiếp hình chóp S.ABCD có chiều cao
và bán kính đáy là
và bán kính đáy là
Suy ra
Ta có SO là trục đường tròn ngoại tiếp hình vuông ABCD. Đường trung trực của SB nằm trong mặt phẳng (SBD) cắt SB, SO lần lượt tại M, I. Ta có IS = IB = IA = IC = ID nên I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
Ta có SI.SO = SM.SB
Suy ra
Do đó V 1 V 2 = 108 25
Phân tích phương án nhiễu.
Phương án A: Sai do HS nhớ nhầm công thức tính thể tích khối cầu là
Do đó tính được V 1 V 2 = 324 25
Phương án B: Sai do HS nhớ nhầm công thức tính thể tích khối nón là
Do đó tính được V 1 V 2 = 18 30 25
Phương án C: Sai do HS nhớ sai công thức tính thể tích khối nón là
Do đó tính được V 1 V 2 = 36 25