Cho biểu thức ![]() trong đó là số thực dương cho trước. Biết rằng giá trị lớn nhất của bằng . Khi đó, mệnh đề nào sau đây đúng?
trong đó là số thực dương cho trước. Biết rằng giá trị lớn nhất của bằng . Khi đó, mệnh đề nào sau đây đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có ln x - y 2 - 2017 x = ln x - y y - 2017 y + e 2018 ⇔ x - y ln x - y - 2017 x - y = e 2018
⇔ ln x - y - e 2018 x - y - 2017 = 0 . Xét hàm số f t = ln t - e 2018 t - 2017 ,có f ' t = 1 t + e 2018 t 2 > 0 ; ∀ t > 0
Suy ra f(t) là hàm số đồng biến trên 0 ; + ∞ mà f e 2018 = 0 ⇒ t = x - y = e 2018
Khi đó P = e 2018 x 1 + x - e 2018 - 2018 x 2 → g x
Lại có g ' x = e 2018 x x 2019 + 2018 x - 2018 e 2018 - 4036 x ⇒ g ' ' < 0 ; ∀ x ∈ - 1 ; 1
Nên g'(x) là hàm số nghịch biến trên [-1;1] mà g ' - 1 = e - 2018 + 2018 > 0
Và g ' 0 = 2019 - 2018 e 2018 < 0 nên tồn tại x 0 ∈ - 1 ; 0 sao cho g ' x 0 = 0
Vậy m a x - 1 ; 1 g x = g x 0 hay giá trị lớn nhất của P đạt được khi x 0 ∈ - 1 ; 0 .

Phương pháp:
+) Lấy loganepe hai vế, đưa phương trình về dạng phương trình bậc hai ẩn x.
+) Tìm điều kiện để phương trình có 2 nghiệm. Áp dụng định lí Vi-ét.
+) Sử dụng BĐT Cô-si cho 3 số không âm đánh giá biểu thức S.
Cách giải:

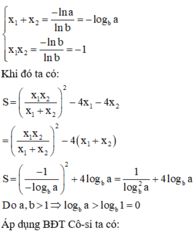
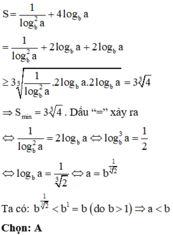

Đáp án A
Ta có
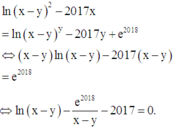
Xét hàm số
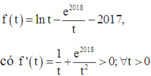
Suy ra f(t) là hàm số đồng biến trên
![]()
Khi đó
![]()
Lại có
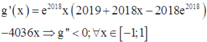
Nên g’(x) là hàm số nghịch biến trên
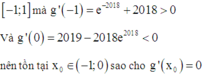
Vậy m a x - 1 ; 1 g ( x ) = g ( x 0 ) hay giá trị lớn nhất của P đạt được khi x 0 ∈ ( - 1 ; 0 )
Đáp án đúng : B