Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a. Biết đường chéo cùa mặt bên là a 3 Khi đó, thể tích khối làng trụ bằng:
A. a 3 3
B. a 3 2
C. a 3 2 3
D. 2 a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

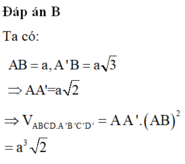

Gọi H là trung điểm BC \(\Rightarrow AH\perp BC\) và \(AH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Áp dụng định lý Pitago cho tam gaics vuông AA'H:
\(A'H=\sqrt{A'A^2-AH^2}=\dfrac{3a}{2}\)
\(V=A'A.S_{ABC}=\dfrac{3a}{2}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{3}}{8}\)

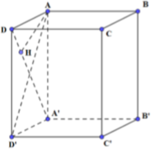
Kẻ
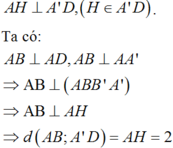
Gọi độ dài đoạn AD là x
∆ A D A ' vuông tại A,
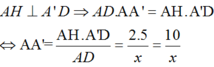
Lại có:
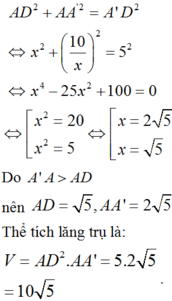
Chọn: C

Đáp án C
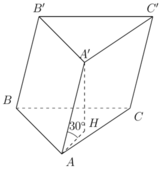
Gọi hình lăng trụ tam giác ABC.A'B'C' có H là hình chiếu vuông góc của A' lên trên mặt phẳng đáy (ABC).
Ta có A B = 3 , A A ' = 2 3 nên A ' H = A A ' . sin 30 ° = 3
Thể tích khối lăng trụ V A B C . A ' B ' C ' = 3 2 3 4 . 3 = 27 4

Đáp án A
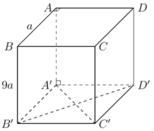
Ta có ABCD.A'B'C'D' là lăng trụ tứ giác đều nên có đáy là hình vuông và cạnh bên vuông góc với đáy.
Suy ra VABCD.A'B'C'D' = SABCD. AA' = a2. 9a = 9a3.

Đáp án C
Diện tích đáy là S = 6. 1 2 a 2 . sin 60 ° = 3 3 a 2 2
Thể tích lăng trụ là V = S h = 3 3 a 2 2 .2 a = 3 3 a 3