Cho tứ diện ABCD với M, N lần lượt là trọng tâm các tam giác ABD, ACD. Xét các khẳng định sau:
(I) MN // mp(ABC).
(II) MN // mp (BCD).
(III) MN // mp(ACD).
(IV) MN // mp(CDA).
A. I, II.
B. II, III.
C. III, IV.
D. I, IV.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 12 2019
Gọi E là trung điểm của AB, M, N lần lượt là trọng tâm của các tam giác ABC, ABD nên:
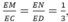
Theo định lí Ta – lét ta có: MN // CD. Vậy MN // (BCD), MN // (ACD).
Đáp án C.
CM
31 tháng 7 2019
Đáp án A.
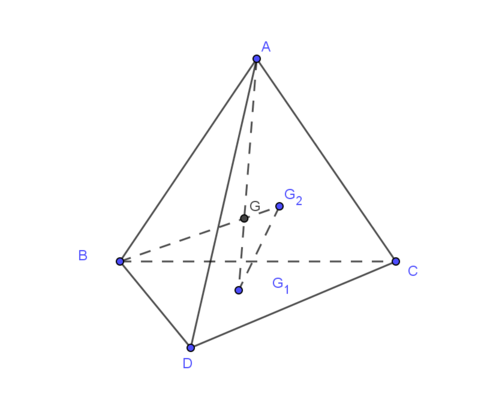
Hình vẽ dễ thấy tính song song là: G 1 G 2 ∥ A B
Chứng minh
Vì G G 1 G A = G G 2 G B = 1 4 ⇒ G 1 G 2 ∥ A B
5 tháng 11 2017
Gọi P và Q lần lượt là trung điểm của AC' và CA'.
CC' giao MN tại I
Xét tam giác AC'C. P là trung điểm AC', M là trung điểm của AC
=> PM là đường trung bình tam giác AC'C => PM//CC'
hay C'I//PM
C' là trọng tâm tam giác ABD => C'N=AN/3.(T/c trọng tâm)
Mà P là trung điểm AC' => C' là trung điểm PN.
Xét tam giác PNM: C' là trung điểm PN, C'I//PM => I là trung điểm của MN
=> CC' đi qua trung điểm của MN (1)
Tương tự ta chứng minh được AA' đi qua trung điểm MN (2)
Tương tự xét trong tam giác DMB: BB' và DD' cùng đi qua trung điểm I của MN (3)
Từ (1),(2) và (3) => AA';BB';CC';DD',MN đồng quy (đpcm).
13 tháng 7 2021
Bn ơi!
Chứng minh AA' đi qua trung điểm MN làm cách nào vậy ạ!
CM
19 tháng 10 2017
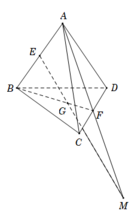
Vì G là trọng tâm tam giác BCD và F là trung điểm của CD nên G thuộc (ABF)
Ta có E là trung điểm của AB nên E thuộc ( ABF).
Gọi M là giao điểm của EG và AF mà A F ⊂ A C D suy ra M thuộc (ACD).
Vậy giao điểm của EG và mp (ACD) là giao điểm M của EG và AF
Chọn B.
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2023
Khẳng định thứ (III) kia chính xác là gì nhỉ? Chắc chắn 30G là ko hợp lý rồi
Chọn A.
- Gọi I là trung điểm của AD.
- Do M, N là trọng tâm tam giác ABD, ACD nên:
- Theo định lý Talet có: MN // BC.
- Mà: BC ⊂ (BCD), BC ⊂ (ABC).
- Vậy: MN // (BCD); MN // (ABC).