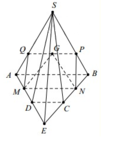
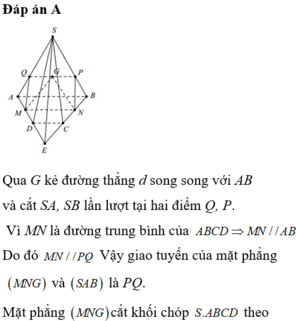
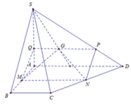
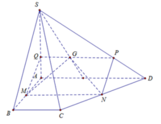
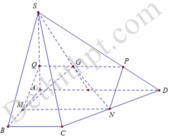
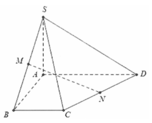
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD. Gọi M, N lần lượt là trung điểm của AD và BC; gọi G là trọng tâm tam giác SAB. Thiết diện của hình chóp với mặt phẳng (MNG) là hình bình hành thì
A. AB = 3CD
B. AB = 2CD
C. CD = 3AB
D. CD = 2AB








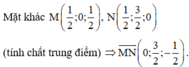
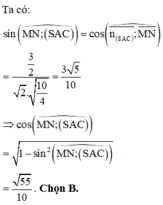
Chọn A