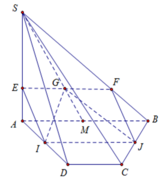
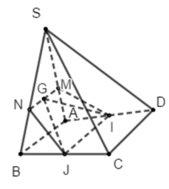
Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm của các tam giác SAB và SAD. E, F lần lượt là trung điểm của AB và AD. Trong các mệnh đề sau, mệnh đề nào đúng?
A. IJ // (SBD)
B. IJ // (SEF)
C. IJ // (SAB)
D. IJ // (SAD)

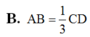
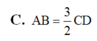
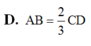



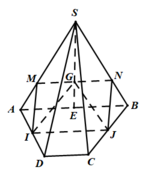




Đáp án A
Tam giác SAB có I là trọng tâm và E là trung điểm của AB
Nên ta có S I S E = 2 3 (1)
Tam giác SAD có J là trọng tâm và F là trung điểm của AD
Nên ta có S J S F = 2 3 (2)
Từ (1) và (2) ta có: IJ // EF (3) (định lý Ta-lét trong tam giác SEF)
Tam giác ABD có EF là đường trung bình nên EF // BD (4)
Từ (3) và (4) suy ra IJ // BD
Mà BD (SBD)
Do đó IJ // (SBD).