Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Góc giữa AB và CD là?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
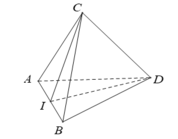
- Gọi I là trung điểm của AB. Vì ABC và ABD là các tam giác đều, nên: 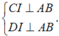
- Suy ra : 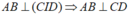
- Vậy góc giữa hai đường thẳng AB và CD bằng 90°

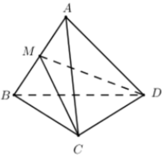
Gọi M là trung điểm AB
\(\Rightarrow\left\{{}\begin{matrix}CM\perp AB\\DM\perp AB\end{matrix}\right.\) (trong tam giác đều trung tuyến đồng thời là đường cao)
\(\Rightarrow AB\perp\left(CDM\right)\)
\(\Rightarrow AB\perp CD\)

Chọn B.
Phương pháp:
Ta xác định tâm mặt cầu ngoại tiếp tứ diện ABCD chính là điểm cách đều bốn đỉnh A, B, C, D.
Dựa vào tính chất tam giác cân, hai tam giác bằng nhau, tỉ số lượng giác để chứng minh các đoạn thẳng bằng nhau từ đó tìm được tâm mặt cầu.
Cách giải:
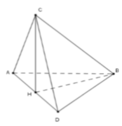
Các tam giác đều ABC và BCD có cạnh 2
⇒ B D = D C = B C = A B = A C = 2
Nên tam giác CAD cân tại C và tam giác BAD cân tại B.

Từ (1) và (2) suy ra tam giác CHB vuông cân tại H có cạnh huyền CB = 2.

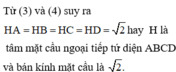

Phương pháp
+) Dựng E sao cho ABCE là hình bình hành. Chứng minh d(AB;CD) = d(M;(CDE)).
+) Dựng khoảng cách từ M đến (CDE).
+) Áp dụng định lí Pytago trong các tam giác hình vuông tính CD.
Cách giải
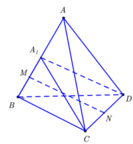
Dựng E sao cho ABCE là hình bình hành như hình vẽ.



a: Gọi E là trung điểm của AB
ΔABC đều nên CE vuông góc AB
ΔABD đều nên DE vuông góc AB
=>AB vuông góc (CDE)
=>AB vuông góc CD
b: Xét ΔCAB có CN/CB=CM/CA
nên MN//AB và MN=1/2AB
Xét ΔDAB có DQ/DA=DP/DB
nên PQ//AB và PQ/AB=DQ/DA=1/2
=>MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Xét ΔADC có AQ/AD=AM/AC
nên QM//DC
=>QM vuông góc AB
=>QM vuông góc QP
=>MNPQ là hình chữ nhật
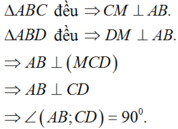
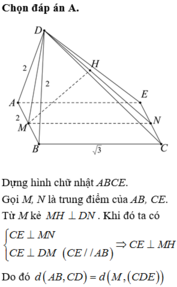
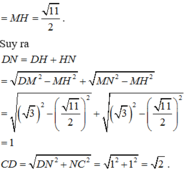
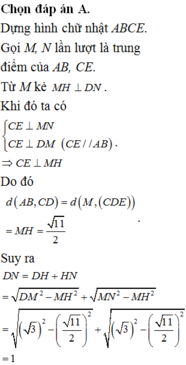





- Gọi I là trung điểm của AB. Vì ABC và ABD là các tam giác đều nên:
- Suy ra: AB ⊥ (CID) ⇒ AB ⊥ CD.
- Do đó, góc giữa AB và CD bằng 90 ° .