Tập hợp các điểm biểu diễn số phức z thỏa mãn 2|z-1| = |z + z ¯ +2| trên mặt phẳng tọa độ là một
A. đường thẳng.
B. đường tròn.
C. parabol.
D. hypebol.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
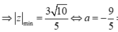
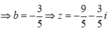
Đặt ![]()
Đặt ![]() Số phức w được biểu diễn bởi điểm M(x';y')
Số phức w được biểu diễn bởi điểm M(x';y')
Em có:

Em có: ![]()
![]()
Mà x = 3y + 2 nên w = ![]()
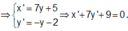
Vậy số phức w được biểu diễn bởi đoạn thẳng: x + 7y + 9 = 0

Đáp án C
Đặt z = x + yi , x ; y ∈ ℝ .
Đặt w = x ' + y ' i , x ' , y ' ∈ ℝ . Số phức w được biểu diễn bởi điểm M x ' ; y ' .
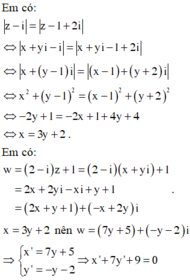
Vậy số phức w được biểu diễn bởi đoạn thẳng: x + 7 y + 9 = 0. .

Chọn đáp án B.
Phương pháp: Tìm tập hợp các điểm biểu diễn số phức z thỏa mãn hệ thức cho trước
+ Đặt ![]()
+ Chuyển hệ thức với z về hệ thức với a, b, rút gọn để tìm hệ thức liên hệ giữa a và b
⇒ Phương trình (đường thẳng, đường tròn) cần tìm.
Cách giải
Giả sử ![]() . Ta có
. Ta có
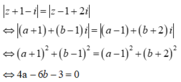

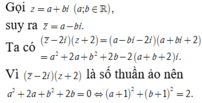
Vậy tập hợp tất cả các điểm biễu diễn số phức z là một đường tròn có bán kính bằng 2 . Chọn B.

Đáp án C
Đặt ![]() Số phức w được biểu diễn bởi điểm M (x;y).
Số phức w được biểu diễn bởi điểm M (x;y).
Ta có:
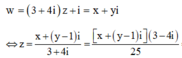
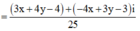
=> |z| = 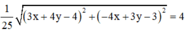
![]()
![]()
![]()
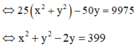
![]()
Vậy số phức w được biểu diễn bởi đường tròn tâm I (0;1), bán kính R = 20 và có phương trình: ![]()
Đáp án C.
Đặt z = a + bi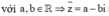
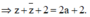
Ta có: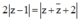
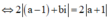
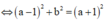
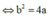
Vậy quỹ tích là một parabol