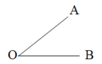
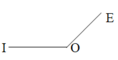
Trong các góc sau, góc nào là góc tù? A. Góc AOB B. Góc COD C. Góc IOE D. Góc XOY...
Đọc tiếp
Trong các góc sau, góc nào là góc tù?
A. Góc AOB
B. Góc COD
C. Góc IOE
D. Góc XOY
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
13 tháng 8 2019
a) Ta có : \(\hept{\begin{cases}\widehat{AOB}=90^o+\widehat{AOC}\\\widehat{COD}=90^o-\widehat{BOC}\end{cases}\Rightarrow\widehat{AOB}+\widehat{COD}=90^o+\widehat{AOC}+90^o-\widehat{BOC}=180^o\Rightarrowđpcm}\)
b) Ta có : \(\widehat{BOC}=\widehat{AOD}\) (cùng phụ nhau với \(\widehat{COD}\))
\(\Rightarrow\frac{\widehat{BOC}}{2}=\frac{\widehat{AOD}}{2}\Rightarrow\widehat{COM}=\widehat{AON}\) (phân giác On và On)
Lại có : \(\widehat{CON}+\widehat{AON}=90^o\Rightarrow\widehat{CON}+\widehat{COM}=90^o\) hay \(\widehat{mOn}=90^o\)
\(\Rightarrow Om\perp On\left(đpcm\right)\)
A
20 tháng 6 2021
a) Ta có : \(OC\perp OA\Rightarrow\widehat{AOC}=90^O\)
\(OD\perp OB\Rightarrow\widehat{BOD}=90^O\)
Các tia OC , OD nằm trong \(\widehat{AOB}\)nên :
\(\widehat{AOD}\)\(=\widehat{AOB}\)\(-\widehat{BOD}\)\(=\widehat{AOB}\)\(-90^O\)
\(\widehat{BOC}=\widehat{AOB}-\widehat{AOC}=\widehat{AOB}-90^O\)
\(\Rightarrow\widehat{AOB}=\widehat{BOC}\)
b) Vì \(\widehat{AOC}< \widehat{AOB}\)( góc vuông nhỏ hơn góc tù )
=> OC nằm giữa hai tia OA và OB.
Vì \(\widehat{BOD}< \widehat{AOB}\)( góc vuông nhỏ hơn góc tù )
=> OD nằm giữa hai tia OA và OB
=> OC và OD nằm giữa hai tia OA và OB
=> Phân giác OM của \(\widehat{COD}\)nằm giữa hai tia OA và OB. ( 1)
Lại có : \(\widehat{MOC}=\widehat{MOD}\)
Theo chứng minh trên ta có : \(\widehat{BOC}=\widehat{AOD}\Rightarrow\widehat{MOC}+\widehat{BOC}=\widehat{MOD}+\widehat{AOD}hay\widehat{MCB}=\widehat{MOA}\)( 2 )
Từ (1) và (2) => OM là tia phân giác của \(\widehat{AOB}\)
# Aeri #
20 tháng 6 2021
Ta có: OC⊥OAOC⊥OA nên ˆAOC=900AOC^=900
OD⊥OBOD⊥OB nên ˆBOD=900BOD^=900 các tia OC, OD ở trong góc AOB nên:
ˆAOD=ˆAOB−ˆBOD=ˆAOB−900AOD^=AOB^−BOD^=AOB^−900
ˆBOC=ˆAOB−ˆAOC=ˆAOB−900BOC^=AOB^−AOC^=AOB^−900
⇒ˆAOD=ˆBOC⇒AOD^=BOC^
b.
Vì ˆAOC<ˆAOBAOC^<AOB^ (góc vuông nhỏ hơn góc tù)
⇒OC⇒OC nằm giữa hai tia OA và OB.
ˆBOD<ˆAOBBOD^<AOB^ (góc vuông nhỏ hơn góc tù)
⇒OD⇒OD nằm giữa hai tia OA và OB
⇒OC⇒OC và OD nằm giữa hai tia OA và OD
⇒⇒ Phân giác OM của góc ˆCODCOD^ nằm giữa hai tia OA và OB (*)
Mặt khác: Do OM là phân giác của góc ˆCODCOD^ nên ˆMOC=ˆMODMOC^=MOD^
Theo chứng minh trên, ta có:
ˆBOC=ˆAOD⇒ˆMOC+ˆBOC=ˆMOD+ˆAODBOC^=AOD^⇒MOC^+BOC^=MOD^+AOD^ hay ˆMCB=ˆMOAMCB^=MOA^ (**)
Từ (*) và (**) ⇒OM⇒OM là tia phân giác góc AOB.
Đáp án C