Cho tam giác ABC vuông taiA ,có độ dài cạnh AB=3cm,cạnh AC=4cm.Gọi AH là đường cao của tam giác .Tính diện tích tam giác AHC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: BC=căn 3^2+4^2=5cm
AH=3*4/5=2,4cm
c: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
=>S AHB/S CHA=(AB/CA)^2=9/16

Câu 1:
a: AH=3x4:5=2,4(cm)
b: HC=16:5=3,2(cm)
Xét ΔAHC vuông tại H có
\(\sin HAC=\dfrac{HC}{AC}=\dfrac{3.2}{4}=\dfrac{4}{5}\)
nên \(\widehat{HAC}=53^0\)

b: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE

Vẽ hình cho 0,5 điểm, câu a/ 1 điểm, câu b/ 1 điểm.
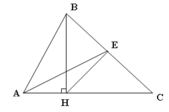
a/ . Gọi S là diện tích:
Ta có: SBAHE = 2 SCEH
Vì BE = EC và hai tam giác BHE, HEC có cùng chiều cao hạ từ đỉnh chung H nên SBHE = SHEC
Do đó SBAH = SBHE = SHEC
Suy ra: SABC = 3SBHA và AC = 3HA ( vì hai tam giác ABC và BHA có cùng chiều cao hạ từ đỉnh chung B)
Vậy HA = = 6 : 3 = 2 ( cm)
Nghĩa là điểm H phải tìm cách A là 2cm
b/ Ta có: SABC = 6 x 3 : 2 = 9 ( cm2)
Vì BE = EC và hai tam giác BAE, EAC có cùng chiều cao hạ từ đỉnh chung A, nên SBAE = SEAC do đó:
SEAC = SABC = 9 : 2 = 4,5 (cm2)
Vì SHEC = SABC = 9 : 3 = 3 (cm2)
Nên SAHE = 4,5 – 3 = 1,5 (cm2)

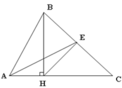
a. Gọi S là diện tích:
Ta có: S B A H E = 2 S C E H
Vì BE = EC và hai tam giác BHE, HEC có cùng chiều cao hạ từ đỉnh chung H nên S B H E = S H E C
Do đó S B A H = S B H E = S H E C
Suy ra: S A B C = 3 S B H A và AC = 3HA ( vì hai tam giác ABC và BHA có cùng chiều cao hạ từ đỉnh chung B)
Vậy HA = A C 3 = 6 : 3 = 2 ( cm)
Nghĩa là điểm H phải tìm cách A là 2cm
b. Ta có: S A B C = 6 x 3 : 2 = 9 ( c m 2 )
Vì BE = EC và hai tam giác BAE, EAC có cùng chiều cao hạ từ đỉnh chung A, nên SBAE = SEAC do đó:
S E A C = 1 2 S A B C = 9 : 2 = 4,5 ( c m 2 )
Vì S H E C = 1 3 S A B C = 9 : 3 = 3 ( c m 2 )
Nên S A H E = 4,5 – 3 = 1,5 ( c m 2 )
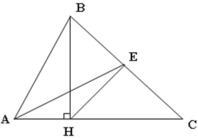


\(S_{AHC}=\dfrac{AH\cdot HC}{2}=\dfrac{2.4\cdot3.2}{2}=2.4\cdot1.6=3.84\left(cm^2\right)\)
Xét \(\Delta ABC\) vuông tại A có
\(BC^2=AB^2+AC^2=25\)
\(\Rightarrow BC=5\left(cm\right)\)
AC\(^2\) = CH . CB = 5 CH
\(\Rightarrow CH=3,2\left(cm\right)\)
AB . AC = AH . BC \(\Rightarrow AH=2,4\)
Nên \(S_{AHC}=\dfrac{1}{2}.AH.CH=\dfrac{1}{2}.2,4.3,2=3,84\left(cm^2\right)\)