Mik cần trình bày rõ ràng ạ, mik cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


( x + 2,7 ) : 4,9 = 25,3
( x + 2,7 ) = 25,3 x 4,9
x + 2,7 = 123,97
x = 123,97 - 2,7
x = 121,27
(x+2,7):4,9=25,3
x+2,7 =25,3x4,9
x+2,7 =123,97
x =123,97-2,7
x =121,27

a) \(\dfrac{x+9}{x^2-9}\)-\(\dfrac{3}{x^2+3x}\) = \(\dfrac{x+9}{\left(x-3\right)\left(x+3\right)}\)-\(\dfrac{3}{x\left(x+3\right)}\)
= \(\dfrac{x^2+9x-3x+9}{x\left(x-3\right)\left(x+3\right)}\)
= \(\dfrac{x^2+6x+9}{x\left(x-3\right)\left(x+3\right)}\)
= \(\dfrac{\left(x+3\right)^2}{x\left(x-3\right)\left(x+3\right)}\)
= \(\dfrac{x+3}{x\left(x-3\right)}\)

Câu 5:
a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó: AHMK là hình chữ nhật

a: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)
b: \(=\dfrac{x^2-2x-3+x^2+2x-3+2x-2x^2}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
c: \(=\dfrac{6-7+x}{3\left(x-1\right)}=\dfrac{x-1}{3\left(x-1\right)}=\dfrac{1}{3}\)
d: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

\(\dfrac{x+9}{x^2-9}-\dfrac{3}{x^2+3x}\)
= \(\dfrac{x+9}{\left(x-3\right).\left(x+3\right)}-\dfrac{3}{x.\left(x+3\right)}\)
=\(\dfrac{\left(x+9\right).x}{\left(x-3\right).\left(x+3\right).x}-\dfrac{3.\left(x-3\right)}{x.\left(x+3\right).\left(x-3\right)}\)
=\(\dfrac{x^2+9x}{x\left(x-3\right)\left(x+3\right)}-\dfrac{3x-9}{x\left(x-3\right)\left(x+3\right)}\)
=\(\dfrac{x^2+9-3x+9}{x\left(x-3\right)\left(x+3\right)}\)
=\(\dfrac{x^2-3x+18}{3\left(x-3\right)\left(x+3\right)}\)
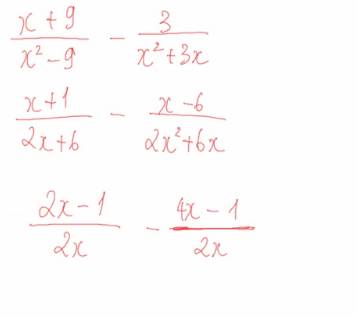
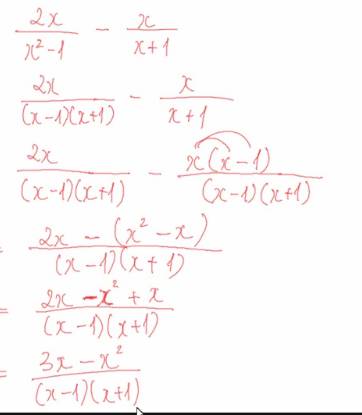




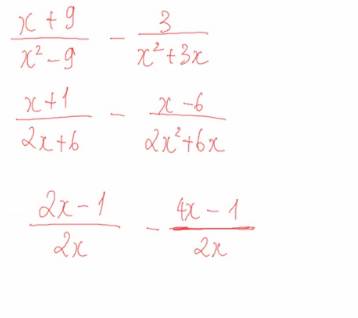
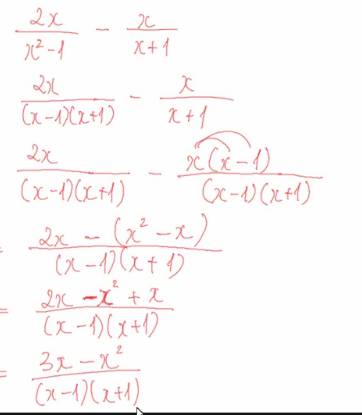
Ta có:
\(A=\dfrac{\sqrt{x}-x}{\sqrt{x}-1}=\dfrac{-\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}=-\sqrt{x}\)
Vậy \(A=-\sqrt{x}\)
\(A=\dfrac{-\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}=-\sqrt{x}\)