Cho đường tròn tâm O, bán kính R = 6cm ngoại tiếp tam giác ABC vuông tại A có AB = 6cm, AC = 8 cm. Trong các dây AB, BC và AC thì dây nào gần tâm hơn?
A. AB
B. BC
C. AC
D. chưa kết luận được.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 12 2017
Đáp án C
Tam giác ABC có góc A là góc tù nên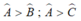 
Mà cạnh đối diện với góc A là cạnh BC .
Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:
BC > AC và BC > AB
Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.
Chưa thể kết luận dây nào xa tâm nhất.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
15 tháng 10 2016
c/ Nối MA; MD; ME ta có
^DME=^DMA+^CMA (1)
^DMA=90 (góc nội tiếp chắn nửa đường tròn (B)) (2)
^CMA=90 (góc nội tiếp chắn nửa đường tròn (C)) (3)
Từ (1) (2) (3) => ^DME=90 độ => D, M, E thẳng hàng
29 tháng 8 2021
Tâm đường tròn ngoại tiếp tam giác ABC nằm trên trung điểm BC
=> Tâm đường tròn là điểm M
CC
10 tháng 12 2020
b) Gọi OD ⊥ AC tại I ( I thuộc OD)
Có: OD⊥ AC (gt) và CB⊥ AC ( △ABC vuông tại C)
Do đó OD // CB
Xét △ABC, có:
OD// CB (cmt)
O là trung điểm AB ( AB là đường kính)
Do đó OI là đường trung bình ABC
=>I là trung điểm AC
Có: OD ⊥ AC(gt) , I trung điểm AC (cmt) (I thuộc OD)
Nên OD là đường trung trực của AC
c)
Xét t/giác AOC, có:
AO=OC (=R)
Do đó t/giác AOC cân tại O
Mà OI ⊥ AC
Nên OI cũng là đường phân giác góc AOC
=> AOI = COI
Xét t/giác ADO và t/giác DOC, có:
OD chung
AOI = COI (cmt)
OA=OC (=R)
Do đó t/giác ADO = t/giác CDO (c-g-c)
=> DAO = DCO
Mà DAO= 90
Nên DCO = 90
Có C thuộc (O) ( dây cung BC)
Nên CD là tiếp tuyến
Đáp án B
Áp dụng định lí Pytago vào tam giác ABC ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100 nên BC =10 cm
Ta có: AB < AC < BC ( 6 cm < 8 cm < 10 cm )
Do đó, dây BC gần tâm nhất, dây AB xa tâm nhất