Rút gọn biểu thức B = x x - 4 1 x - 2 1 x 2 với x

PT

Pham Trong Bach

26 tháng 11 2018

Rút gọn biểu thức B = x x - 4 + 1 x - 2 + 1 x + 2 với x > 0, x ≠ 4. A. B = x x + 2 B. B = x x - 2 C. B = - x x - 2 D. B = 2 x x - 2 ...

Đọc tiếp

#Toán lớp 9

1

CM

Cao Minh Tâm

26 tháng 11 2018

Đúng(0)

HT

Hồng Trần

16 tháng 2 2022

Rút gọn biểu thức P = √x/ √x-2 /(x-2/x-4 - 1/ √x+2 với x>0;x khác 1, x khác 4

#Toán lớp 9

1

N

nthv_.

16 tháng 2 2022

Bạn viết lại đề bài nhé!

Đúng(0)

ND

Nguyễn Đức Thanh

22 tháng 1 2022 - olm

2, a) Rút gọn biểu thức 1 3 2 2 : 2 2 2 4 x x x x B x x x x                 (với x x   0; 4 ) b) Tìm x để B >1

#Toán lớp 9

0

HT

Hồng Trần

20 tháng 3 2022

Cho biểu thức B=1/x+√x + 2√x/x-1 - 1/x-√x với x>0 và x khác 1 .Rút gọn biểu thức

#Toán lớp 9

0

KK

Kim Khánh Linh

15 tháng 5 2021 - olm

Cho hai biểu thức: $A=\dfrac{\sqrt{x}}{\sqrt{x}+2}$ và $B=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}$ với $x>0$ và $x \neq 4$

1) Tính giá trị của biểu thức $A$ khi $x=9$.

2) Rút gọn biểu thức $B$.

3) Chứng minh: $\dfrac{A}{B}>-1$, với $x>0$ và $x \neq 4$.

#Toán lớp 9

2

B

Bellion

15 tháng 5 2021

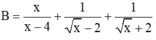
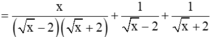
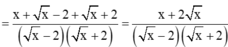
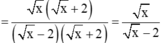
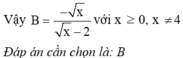
Bài làm :

1) Khi x=9 ; giá trị của A là :

$A=\frac{\sqrt{9}}{\sqrt{9}+2}=\frac{3}{3+2}=\frac{3}{5}$

2) Ta có :

$B=...$

$=\frac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\frac{1.\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\frac{1.\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x+2}\right)}$

$=\frac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}$

$=\frac{x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}$

$=\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}$

$=\frac{\sqrt{x}}{\sqrt{x}-2}$

3) Ta có :

$\frac{A}{B}=\frac{\sqrt{x}}{\sqrt{x}+2}\div\frac{\sqrt{x}}{\sqrt{x}-2}=\frac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\sqrt{x}}=\frac{\sqrt{x}-2}{\sqrt{x}+2}=\frac{\sqrt{x}+2-4}{\sqrt{x}+2}=1-\frac{4}{\sqrt{x}+2}$

Xét :

$\frac{A}{B}+1=\frac{4}{\sqrt{x+2}}>0\Rightarrow\frac{A}{B}>-1$

=> Điều phải chứng minh

Đúng(0)

PT

Phùng Thị Uyên

4 tháng 6 2021

1, thay x=9(TMĐKXĐ) vào A ta đk:

A=$\dfrac{\sqrt{9}}{\sqrt{9}-2}=3$

vậy khi x=9 thì A =3

2,với x>0,x≠4 ta đk:

B=$\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-2}$

vậy B=$\dfrac{\sqrt{x}}{\sqrt{x}-2}$

3,$\dfrac{A}{B}>-1$ (x>0,x≠4)

⇒$\dfrac{\sqrt{x}}{\sqrt{x}+2}:\dfrac{\sqrt{x}}{\sqrt{x}-2}>-1\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}+2}.\dfrac{\sqrt{x}-2}{\sqrt{x}}>-1\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}+2}>-1$

⇒$\sqrt{x}-2>-1$ (vì $\sqrt{x}+2>0$)

⇔$\sqrt{x}>1$⇔x=1 (TM)

vậy x=1 thì $\dfrac{A}{B}>-1$ với x>0 và x≠4

Đúng(0)

NN

NGUYỄN NGỌC DIỆU

18 tháng 4 2023

Cho biểu thức A=2√x - 3/√x - 2 và B=2/√x+3 + √x/√x-3 + 4√x/9-x với x≥0; x≠4; x≠9. a) tính giá trị biểu thức A khi x thỏa mãn |x-2|=2. b) rút gọn biểu thức B. c) đặt C=A.B. Tìm x để C≥1.

#Toán lớp 9

2

2611

18 tháng 4 2023

`a)|x-2|=2<=>[(x=4(ko t//m)),(x=0(t//m)):}`

Thay `x=0` vào `A` có: `A=[2\sqrt{0}-3]/[\sqrt{0}-2]=3/2`

`b)` Với `x >= 0,x ne 4` có:

`B=[2(\sqrt{x}-3)+\sqrt{x}(\sqrt{x}+3)-4\sqrt{x}]/[(\sqrt{x}+3)(\sqrt{x}-3)]`

`B=[2\sqrt{x}-6+x+3\sqrt{x}-4\sqrt{x}]/[(\sqrt{x}+3)(\sqrt{x}-3)]`

`B=[x+\sqrt{x}-6]/[(\sqrt{x}+3)(\sqrt{x}-3)]`

`B=[(\sqrt{x}+3)(\sqrt{x}-2)]/[(\sqrt{x}+3)(\sqrt{x}-3)]`

`B=[\sqrt{x}-2]/[\sqrt{x}-3]`

`c)` Với `x >= 0,x ne 4` có:

`C=A.B=[2\sqrt{x}-3]/[\sqrt{x}-2].[\sqrt{x}-2]/[\sqrt{x}-3]=[2\sqrt{x}-3]/[\sqrt{x}-3]`

Có: `C >= 1`

`<=>[2\sqrt{x}-3]/[\sqrt{x}-3] >= 1`

`<=>[2\sqrt{x}-3-\sqrt{x}+3]/[\sqrt{x}-3] >= 0`

`<=>[\sqrt{x}]/[\sqrt{x}-3] >= 0`

Vì `x >= 0=>\sqrt{x} >= 0`

`=>\sqrt{x}-3 > 0`

`<=>x > 9` (t/m đk)

Đúng(2)

NL

Nguyễn Lê Phước Thịnh

18 tháng 4 2023

loading...

Đúng(1)

VL

việt lê

19 tháng 1 2022

Bài 1: Cho biểu thức: A= (x^2-3/x^2-9 + 1/x-3):x/x+3 a, Rút gọn A. b, Tìm các giá trị của x để A = 3Bài 2: Cho biểu thức: A = (x/x^2-4 + 1/x+2 - 2/x-2) : (1- x/x+2) Với x khác 2 và -2 a, Rút gọn biểu thức, b, Tìm các giá trị nguyên của x để A nhận giá trị nguyên.Bài 3: Cho biểu thức A = 2x/x+3 + x+1/x-3 + 3x-11x/9-x^2, với x khác 3 , -3 a, Rút gọn biểu thức A. b, Tính giá trị...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

19 tháng 1 2022

Bài 1:

a: $A=\dfrac{x^2-3+x+3}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x}=\dfrac{x\left(x+1\right)}{x\left(x-3\right)}=\dfrac{x+1}{x-3}$

b: Để A=3 thì 3x-9=x+1

=>2x=10

hay x=5

Bài 2:

a: $A=\dfrac{x+x-2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x+2-x}{x+2}$

$=\dfrac{-6}{x-2}\cdot\dfrac{1}{2}=\dfrac{-3}{x-2}$

b: Để A nguyên thì $x-2\in\left\{1;-1;3;-3\right\}$

hay $x\in\left\{3;1;5;-1\right\}$

Đúng(1)

PT

Pham Trong Bach

29 tháng 8 2019

Rút gọn biểu thức: P = x − x + 2 x − x − 2 − x x − 2 x : 1 − x 2 − x với x > 0 ; x ≠ 1 ; x ≠ 4

#Toán lớp 9

1

CM

Cao Minh Tâm

29 tháng 8 2019

Ta có: P = x − x + 2 ( x + 1 ) ( x − 2 ) − x x ( x − 2 ) : 1 − x 2 − x = x − x + 2 − x ( x + 1 ) ( x + 1 ) ( x − 2 ) . 2 − x 1 − x = 2 − 2 x ( x + 1 ) ( x − 1 ) = 2 ( 1 − x ) ( x + 1 ) ( x − 1 ) = − 2 x + 1

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP