Cho hàm số y = x 3 + x + 2 có đồ thị (C). Số giao điểm của (C) và đường thẳng y = 2 là:
A. 1.
B. 0.
C. 3.
D. 2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
và đường thẳng y = x + 2 là:
CM
22 tháng 7 2019
Phương trình hoành độ giao điểm
x3+2mx2+3(m-1)x+2 =-x+2 hay x(x2+2mx+3(m-1))=0
suy ra x=0 hoặc x2+2mx+3(m-1)=0 (1)
Đường thẳng d cắt (C) tại ba điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 0
⇔ m 2 - 3 m + 3 > 0 m - 1 ≠ 0 ⇔ ∀ m m ≠ 1 ⇔ m ≠ 1
Khi đó ta có: C( x1 ; -x1+2) ; B(x2 ; -x2+2) trong đó x1 ; x2 là nghiệm của (1) ; nên theo Viet thì x 1 + x 2 = - 2 m x 1 x 2 = 3 m - 3
Vậy
C B → = ( x 2 - x 1 ; - x 2 + x 1 ) ⇒ C B = 2 ( x 2 - x 1 ) 2 = 8 ( m 2 - 3 m + 3 )
d ( M ; ( d ) ) = - 3 - 1 + 2 2 = 2
Diện tích tam giác MBC bằng khi và chỉ khi
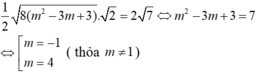
Chọn B.
CC
10 tháng 12 2020
a)
Thay x=0 vào hàm số y= 3x+3, ta được: y= 3 x 0 + 3 = 3
Thay y=0 vào hàm số y= 3x+3, ta được: 0= 3x+3 => x= -1
Vậy đồ thị hàm số đi qua điểm B(-1;0) và C(0;3)
Thay x=0 vào hàm số y= -x+1, ta được: y= -0 + 1 = 1
Thay y=0 vào hàm số y= -x+1, ta được: 0= -x+1 => x= 1
(Có gì bạn tự vẽ đồ thị nha :<< mình không load hình được sorry bạn nhiều)
b) Hoành độ giao điểm của hai đường thằng y=3x+3 và y=-x+1 :
3x+3 = -x+1
<=> 3x + x = 1 - 3
<=> 4x = -2
<=> x= - \(\dfrac{1}{2}\)
Thay x= - \(\dfrac{1}{2}\) vào hàm số y= -x+1, ta được: y= \(\dfrac{1}{2}\)+1 = \(\dfrac{3}{2}\)
Vậy giao điểm của hai đường thằng có tọa độ (\(-\dfrac{1}{2};\dfrac{3}{2}\))
c) Gọi góc tạo bởi đường thẳng y= 3x+3 là α
OB= \(\left|x_B\right|=\left|-1\right|=1\)
OC= \(\left|y_C\right|=\left|3\right|=3\)
Xét △OBC (O= 90*), có:
\(tan_{\alpha}=\dfrac{OC}{OB}=\dfrac{3}{1}=3\)
=> α= 71*34'
Vậy góc tạo bởi đường thằng y=3x+3 là 71*34'
CM
12 tháng 3 2018
2x3-3x2+1 =x-1 hay 2x3-3x2-x+2=0
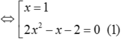
Khi đó ta có A(1 ; 0) ; B( x1 ; x1-1) và C( x2 ; x2-1) ( x1 ; x2 là nghiệm của (1))
Ta có 
, suy ra
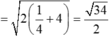
Chọn B.
Đáp án A
Phương trình hoành độ giao điểm là:
x 3 + x + 2 = 2 ⇔ x 3 + x = 0 ⇔ x x 2 + 1 = 0 ⇔ x = 0