Nghiệm của phương trình ln(x+1)=2 là
A. 99
B. e 2 - 1
C. 101
D. e 2 + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 11 2017
Lần lượt thay x = -2 vào từng bất phương trình:
a) -3x + 2 = -3.(-2) + 2 = 8
Vì 8 > -5 nên x = -2 là nghiệm của bất phương trình -3x + 2 > -5.
b) 10 – 2x = 10 – 2.(-2) = 10 + 4 = 14
Vì 14 > 2 nên x = -2 không phải nghiệm của bất phương trình 10 – 2x < 2.
c) x2 – 5 = (-2)2 – 5 = 4 – 5 = -1
Vì -1 < 1 nên x = -2 là nghiệm của bất phương trình x2 – 5 < 1.
d) |x| = |-2| = 2
Vì 2 < 3 nên x = -2 là nghiệm của bất phương trình |x| < 3.
e) |x| = |-2| = 2
Vì 2 = 2 nên x = -2 không phải nghiệm của bất phương trình |x| > 2.
f) x + 1 = -2 + 1 = -1.
7 – 2x = 7 – 2.(-2) = 7 + 4 = 11
Vì -1 < 11 nên x = -2 không phải nghiệm của bất phương trình x + 1 > 7 – 2x.
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2023
ĐKXĐ: \(x\ge-1\)
Đặt \(\sqrt{x+1}=y\ge0\)
\(\Rightarrow4x^2+12xy=27y^2\)
\(\Leftrightarrow\left(2x-3y\right)\left(2x+9y\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3y=2x\\9y=-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3\sqrt{x+1}=2x\left(x\ge0\right)\\9\sqrt{x+1}=-2x\left(x\le0\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}9\left(x+1\right)=4x^2\left(x\ge0\right)\\81\left(x+1\right)=4x^2\left(x\le0\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{81-9\sqrt{97}}{8}\end{matrix}\right.\)
17 tháng 3 2023
a: A=x1+x2=-5/2
b: \(=\dfrac{x_1+x_2}{x_1x_2}=\dfrac{-5}{2}:\left(-1\right)=\dfrac{5}{2}\)
c: \(=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\)
\(=\left(-\dfrac{5}{2}\right)^3-3\cdot\dfrac{-5}{2}\cdot\left(-1\right)\)
\(=-\dfrac{125}{8}-\dfrac{15}{2}=\dfrac{-185}{8}\)
e: \(E=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{\left(-\dfrac{5}{2}\right)^2-4\cdot\left(-1\right)}=\sqrt{\dfrac{25}{4}+4}=\dfrac{\sqrt{41}}{2}\)
, x 
N là:
B. 
C. 
D Một số khác
B. 
C. 
D. Một số khác
= 220 thì n bằng:
CM
6 tháng 9 2019
a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
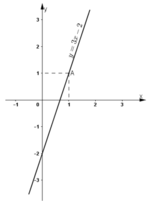
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (2/3 ; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (2/3 ; 0) và (0; -2).
b) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
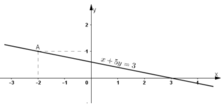
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y=3/5 ⇒ Đường thẳng đi qua điểm (0; 3/5).
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 3/5).
c) 4x – 3y = -1
⇔ 3y = 4x + 1
⇔ 
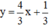
Vậy phương trình có nghiệm tổng quát là (x;4/3x+1/3)(x ∈ R).
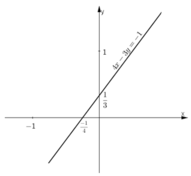
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0;1/3) .
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm (-1/4;0) .
Vậy đường thẳng 4x – 3y = -1 đi qua (0;1/3) và (-1/4;0).
d) x + 5y = 0
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
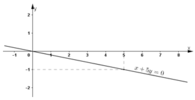
e) 4x + 0y = -2
⇔ 4x = -2 ⇔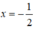 
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
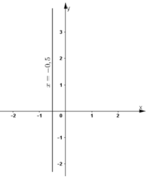
f) 0x + 2y = 5
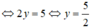
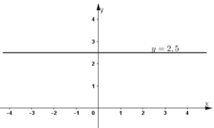
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.
MN
13 tháng 5 2019
\(x^2-\left(2m+3\right)x+m^2+3m+2=0\left(1\right).\)
a, Với m = 1, \(\left(1\right)\Leftrightarrow x^2-7m+6=0\Leftrightarrow\left(m-1\right)\left(m-6\right)\Leftrightarrow\orbr{\begin{cases}m=1\\m=6\end{cases}}\)
b, Với x = 2 \(\left(1\right)\Leftrightarrow4-2\left(2m+3\right)+m^2+3m+2=0\)
\(\Leftrightarrow m^2-m=0\Leftrightarrow m\left(m-1\right)=0\Leftrightarrow\orbr{\begin{cases}m=0\\m=1\end{cases}}\)
Với m = 0, \(\left(1\right)\Leftrightarrow x^2-3x+2=0\Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\orbr{\begin{cases}x=2\\x=1\end{cases}}\)
Với m = 1, \(\left(1\right)\Leftrightarrow x^2-5x+6=0\Leftrightarrow\left(x-3\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x=3\\x=2\end{cases}}\)
c, \(\Delta=4m^2+12m+9-4m^2-12m-8=1>0\)
Vì \(\Delta>0\)nên phương trình có 2 nghiệm phân biệt với mọi m.
MN
13 tháng 5 2019
d, Theo vi-ét ta có: \(\hept{\begin{cases}x_1+x_2=2m+3\left(1\right)\\x_1.x_2=m^2+3m+2\left(2\right)\end{cases}}\)
Ta có: \(x_1^2+x_2^2=1\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=1\)
\(\Leftrightarrow\left(2m+3\right)^2-2\left(m^2+3m+2\right)=1\)
\(\Leftrightarrow4m^2+12m+9-2m^2-6m-4-1=0\)
\(\Leftrightarrow2m^2-6m-4=0\Leftrightarrow m^2-3m-2=0\Leftrightarrow m=\frac{3\pm\sqrt{17}}{2}\)
c, Phương trình có nghiệm này bằng 3 nghiệm kia:\(\Leftrightarrow x_1=3x_2\left(3\right)\)
Kết hợp (1) và (3) ta có hệ : \(\hept{\begin{cases}x_1+x_2=2m+3\\x_1=3x_2\end{cases}\Leftrightarrow\hept{\begin{cases}x_1=\frac{6m+9}{5}\\x_2=\frac{2m+3}{5}\end{cases}}\left(I\right)}\)
Kết hợp (I) và (2) ta được: \(\frac{\left(6m+9\right)\left(2m+3\right)}{25}=m^2+3m+2\)
\(\Leftrightarrow25m^2+75m+50=12m^2+36m^2+27\)
\(\Leftrightarrow13m^2+39m^2+23=0\)
...
Có ln ( x + 1 ) = 2 ⇔ x + 1 = e 2
⇔ x = e 2 - 1
Chọn đáp án B.