Cho hai hình vuông ABCD và ABEF không cùng nằm trên một mặt phẳng. Mệnh đề nào sau đây đúng?
A. AD//BE
B. (DAF)//(CBE)
C. DF//BC
D. (ABD)//(CFE)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 12 2018
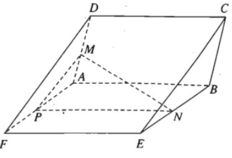
Trong mặt phẳng (ADF), kẻ đường thẳng MP // DF (P ∈ AF)
Ta có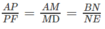 
Nên PN // FE. Do đó (MNP) // (DEF).
Vậy MN song song với mặt phẳng (DEF) cố định.
CM
8 tháng 7 2019
Chọn A
Gọi H là trung điểm AB
nên hình chiếu của SD trên (ABCD) là HD
Tam giác SAB đều cạnh a nên SH = a 3 2
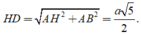
Tam giác vuông SHD
CM
19 tháng 3 2019
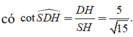
a) Giao tuyến của các cặp mặt phẳng
*Giao tuyến của (AEC) và (BFD)
• Trong hình thang ABCD, AC cắt DB tại G, ta có:
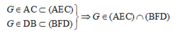
Tương tự, AE cắt BF tại H,
Ta có :
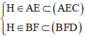⇒ H ∈ (AEC) ∩ (BFD).
Vậy GH = (AEC) ∩ (BFD)
*Giao tuyến của (BCE) và (ADF)
Trong hình thang ABCD, BC cắt AD tại I, ta có: I ∈ (BCE) ∩ (ADF)
Trong hình thang ABEF, BE cắt AF tại K, ta có: K ∈ (BCE) ∩ (ADF)
Vậy IK = (BCE) ∩ (ADF)
b) Giao điểm của AM với mp(BCE)
Trong mp(ADF), AM cắt IK tại N, ta có:
N ∈ IK ⊂ (BCE)
Vậy N = AM ∩ (BCE).
c) Giả sử AC cắt BF.
⇒ Qua AC và BF xác định duy nhất 1 mặt phẳng.
Mà qua A và BF có duy nhất mặt phẳng (ABEF)
⇒ AC ⊂ (ABEF)
⇒ C ∈ (ABEF) (Vô lý).
Vậy AC và BF không cắt nhau.
CM
29 tháng 9 2018
a) Đúng
b) Đúng
c) Sai (vì a có thể nằm trong mp(α), xem hình vẽ)
d) Sai, chẳng hạn hai mặt phẳng (α) và (β) cùng đi qua đường thẳng a và a ⊥ mp(P) nên (α) và (β) cùng vuông góc với mp(P) nhưng (α) và (β) cắt nhau.
e) Sai, chẳng hạn a và b cùng ở trong mp(P) và mp(P) ⊥ d. Lúc đó a và b cùng vuông góc với d nhưng a và b có thể không song song nhau.
Đáp án B
Vì AD // BC
AF // BE
AD, AF là 2 đường thẳng cắt nhau thuộc mp (ADF)
BC, BE là 2 đường thẳng cắt nhau thuộc mp (BCE)
=> (DAF)//(CBE)