Tính : 1 - 1 2 ; 1 2 - 1 3 ; 1 3 - 1 4 ; 1 4 - 1 5 ; 1 5 - 1 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
10 tháng 7 2019
Đúng(0)
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
8 tháng 6 2021
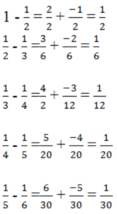
Bạn vui lòng viết đề bằng công thức toán để được hỗ trợ tốt hơn.
LC
1
NH
1
23 tháng 12 2020
uses crt;
var a,m,i:integer;
s:real;
begin
clrscr;
write('Nhap a='); readln(a);
write('Nhap m='); readln(m);
s:=1;
for i:=1 to m do
s:=s+1/sqr(a+i);
writeln(s:4:2);
readln;
end.
SU
1
NH
1
DD
Đoàn Đức Hà
Giáo viên
4 tháng 3 2022
\(\frac{1}{1+2}+\frac{1}{1+2+3}+...+\frac{1}{1+2+...+20}\)
\(=\frac{2}{2\times3}+\frac{2}{3\times4}+...+\frac{2}{20\times21}\)
\(=2\times\left(\frac{1}{2\times3}+\frac{1}{3\times4}+...+\frac{1}{20\times21}\right)\)
\(=2\times\left(\frac{3-2}{2\times3}+\frac{4-3}{3\times4}+...+\frac{21-20}{20\times21}\right)\)
\(=2\times\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{20}-\frac{1}{21}\right)\)
\(=2\times\left(\frac{1}{2}-\frac{1}{21}\right)\)
\(=\frac{19}{21}\)
LM
7 tháng 2 2016
Xét số hạng tổng quát thứ n (n nguyên và n>1), ta có
1/n(1+2+...+n)=[n(n+1)/2]/n= [n(n+1)]/(2n)
Do đó
B = 1 + 1/2 (1 + 2) + 1/3 (1 + 2 + 3) + 1/4 (1 + 2 + 3 +4) + ...+ 1/20 (1 + 2 +... + 20)
=1 +[2(2+1)]/(2.2) +[3(3+1)]/(2.3) +[4(4+1)]/(2.4) +... +[20(20+1)]/(2.20)
=1+3/2 +4/2 +5/2 +... +21/2
=(2+3+4+5+...+20)/2=104,5 . TICH CHON MINH NHA CAC BAN THI CA NAM SE GAP NHIEU DIEU MAY MAN DAY
LM
7 tháng 2 2016
Xét số hạng tổng quát thứ n (n nguyên và n>1), ta có
1/n(1+2+...+n)=[n(n+1)/2]/n= [n(n+1)]/(2n)
Do đó
B = 1 + 1/2 (1 + 2) + 1/3 (1 + 2 + 3) + 1/4 (1 + 2 + 3 +4) + ...+ 1/20 (1 + 2 +... + 20)
=1 +[2(2+1)]/(2.2) +[3(3+1)]/(2.3) +[4(4+1)]/(2.4) +... +[20(20+1)]/(2.20)
=1+3/2 +4/2 +5/2 +... +21/2
=(2+3+4+5+...+20)/2=104,5
