Gọi A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k. Chứng minh rằng nếu M là trung điểm của AB thì M’ = F(M) là trung điểm của A’B’.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
22 tháng 10 2017
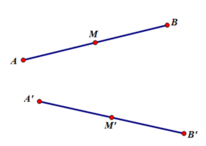
Gọi A', B', M' lần lượt là ảnh của A, B, M qua phép dời hình F
Theo tính chất 1 ⇒ AB = A'B' và AM = A'M' (1)
M là trung điểm AB ⇒ AM = 1/2 AB
Kết hợp (1) ⇒ A'M' = 1/2 A'B' ⇒ M' là trung điểm A'B'

24 tháng 12 2021
a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
Do đó: AEMF là hình chữ nhật
A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k ⇒ A’B’= kAB
M’ = F(M) ⇒ A’M’ = kAM
M là trung điểm AB ⇒ AM = 1/2 AB ⇒ kAM = 1/2 kAB hay A’M’= 1/2 A’B’
Vậy M’ là trung điểm của A’B’