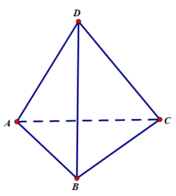
Cho hình tứ diện ABCD. Hãy chỉ ra các vecto có điểm đầu là A và điểm cuối là các điểm còn lại của hình tứ diện. Các vecto đó có cùng nằm trong một mặt phẳng không?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 1 2019
Đáp án A
Hiển nhiên thiết diện của hình tứ diện A B C D khi cắt bởi mặt phẳng M N P là một tam giác
CM
4 tháng 5 2017
Đáp án A
Hiển nhiên thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (MNP) là một tam giác.
CM
7 tháng 8 2017
Các vecto có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng vecto A B → là D C → , A ' B ' → , A ' C ' →
CM
21 tháng 8 2017
Đáp án D.
Phương pháp:
Gọi n → a ; b ; c , n → ≠ 0 → là một VTPT của α . Viết phương trình mặt phẳng α .
Sử dụng các giả thiết O ∈ α ; A ∈ α ; d B ; α = 3 lập hệ phương trình tìm a, b, c.
Cách giải:
Gọi n → a ; b ; c , n → ≠ 0 → là một VTPT của α .
O 0 ; 0 ; 0 ∈ α ⇒ α : a x + b y + c z = 0
A 1 ; 1 ; 0 ∈ α ⇒ a + b = 0 ⇒ b = − a ⇒ α : a x − a y + c z = 0
d B ; α = 3 ⇔ a .0 − a . − 1 + 2 c 2 a 2 + c 2 = 3 ⇔ a + 2 c 2 a 2 + c 2 = 3
⇔ a + 2 c 2 = 3 2 a 2 + c 2 ⇔ a 2 + 4 a c + 4 c 2 = 6 a 2 + 3 c 2 ⇔ 5 a 2 − 4 a c − c 2 = 0
Cho
a = 1 ⇒ c 2 + 4 c − 5 = 0 ⇔ c = 1 c = − 5 ⇒ n → 1 ; − 1 ; 1
hoặc n → 1 ; − 1 ; − 5 .
CM
14 tháng 1 2018
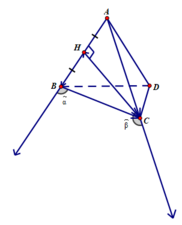
Tứ diện ABCD đều có các mặt là tam giác đều
a) Góc giữa A B → v à B C → là góc α ^ và
α ^ = 180 o - 60 o = 120 o
b) Góc giữa C H → v à A C → là β ^
H là trung điểm cạnh AB của tam giác đều ABC nên CH vừa là trung tuyến vừa là đường cao nên CH ⊥ AB
Xét tam giác vuông ACH tại H có
A C H ^ + H A C ^ = 90 o ⇒ A C H ^ = 90 o - 60 o = 30 o
Nên β ^ = 180 o - 30 o = 150 o
CM
3 tháng 10 2018
Đáp án B
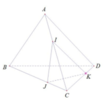
Thiết diện của hình chóp khi cắt bởi mp (IJK) là tam giác IJK.
Các vecto có điểm đầu là A và điểm cuối là các điểm còn lại của hình tứ diện là: A B → , A C → , A D →
Các vecto đó không cùng nằm trong một mặt phẳng