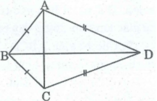
Tứ giác ABCD có AB = BC, CD = DA. Cho biết B = 100 0 , D = 70 0 , tính góc A và góc C.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 7 2019
Bài 1)
a) Vì A: B:C:D = 1:2:3:4
=> A= B/2 = C/3=D/4
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
A = 36 độ
B= 72 độ
C=108 độ
D= 144 độ
b) Ta có :
A + D = 36 + 144 = 180 độ(1)
B+C = 72 + 108 = 180 độ(2)
Từ (1) và (2) ta có:
=> AB //CD (dpcm)
c) Ta có :
CDE + ADC = 180 độ(kề bù)
=> CDE = 180 - 144 = 36
Ta có :
BCD + DCE = 180 độ ( kề bù)
=> DCE = 180 - 108 = 72
Xét ∆CDE ta có :
CDE + DCE + DEC = 180 ( tổng 3 góc trong ∆)
=> DEC = 180 - 72 - 36 = 72 độ
3 tháng 7 2019
Bài 2)
a) Ta có ABCD có :
A + B + C + D = 360 độ
Mà C = 80 độ
D= 70 độ
=> A+ B = 360 - 80 - 70 = 210 độ
Ta có AI là pg góc A
BI là pg góc B
=> DAI = BAI = A/2
=> ABI = CBI = B/2
=> BAI + ABI = A + B /2
=> BAI + ABI = 210/2 = 105
Xét ∆IAB ta có :
IAB + ABI + AIB = 180 độ
=> AIB = 180 - 105
=> AIB = 75 độ
=>
LS
0
CM
24 tháng 6 2019
Đáp án cần chọn là: A
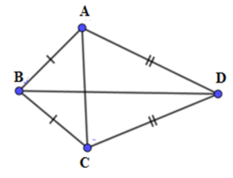
Xét tam giác ABC có: B ^ = 100 ° ; A B = B C
⇒ ∆ A B C cân tại B .
B A C ^ = B C A ^ = 180 0 − 100 0 2 = 40 0
Xét tam giác ADC có C D = D A ⇒ ∆ A D C cân tại D có A D C ^ = 70 ° nên D A C ^ = D C A ^ = 180 0 − 70 0 2 = 55 0
Từ đó ta có A ^ = B A D ^ = B A C ^ + C A D ^ = 40 ° + 55 ° = 95 °
Và C ^ = B C D ^ = B C A ^ + A C D ^ = 40 ° + 55 ° = 75 °
Nên A ^ = C ^ = 95 °
E
7 tháng 5 2017
a) \(a^2+b^2+c^2+d^2=ab+bc+ac+cd.\)
<=>\(2a^2+2b^2+2c^2+2d^2=2ab+2ac+2bc+2cd\)
<=>\(2a^2+2b^2+2c^2+2d^2-2ab-2bc-2ac-2cd=0\)
<=>\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)+\left(d^2-2cd+c^2\right)\)=0
<=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2+\left(d-c\right)^2=0\)
=>a=b=c=d
=> ABCD là hình thoi
27 tháng 7 2016
a, ta có AB bằng BC suy ra B thước đường trung trực AC
AD bằng CD suy ra B thuộc đường trung trực của AC
SUY RA BD thuic đường trung trực của AC
b, xét tam giác ABD và tam giac BCD
AB bằng BC ,AD băng CD , BD chung
suy ra tam giác ABD bằng tam giác BCD
suy ra góc ABD bằng góc BCD
ta có góc ABD +góc BCD bằng 360 -góc B - góc D bằng 360- 100-70 bảng 190 do
suy ra góc A bằng góc C bằng 190:2 bằng 95 độ
-
10 tháng 7 2019
Bài 1)
Trên AD lấy E sao cho AE = AB
Xét ∆ACE và ∆ACB ta có :
AC chung
DAC = BAC ( AC là phân giác)
AB = AE (gt)
=> ∆ACE = ∆ACB (c.g.c)
=> CE = CB (1)
=> AEC = ABC = 110°
Mà AEC là góc ngoài trong ∆EDC
=> AEC = EDC + ECD ( Góc ngoài ∆ bằng tổng 2 góc trong không kề với nó)
=> ECD = 110 - 70
=> EDC = 40°
Xét ∆ EDC :
DEC + EDC + ECD = 180 °
=> CED = 180 - 70 - 40
=> CED = 70°
=> CED = EDC = 70°
=> ∆EDC cân tại C
=> CE = CD (2)
Từ (1) và (2) :
=> CB = CD (dpcm)
b) Ta có thể thay sao cho tổng 2 góc đối trong hình thang phải = 180°
Xét ∆ BAD và ∆ BCD, ta có:
BA = BC (gt)
DA = DC (gt)
BD cạnh chung
Suy ra: ∆ BAD = ∆ BCD (c.c.c)
⇒ ∠ (BAD) = ∠ (BCD)
Mặt khác, ta có: ∠ (BAD) + ∠ (BCD) + ∠ (ABC) + ∠ (ADC) = 360 0
Suy ra: ∠ (BAD) + ∠ (BCD) = 360 0 – ( ∠ (ABC) + ∠ (ADC) )
2 ∠ (BAD) = 360 0 - 100 0 + 70 0 = 190 .
⇒ ∠ (BAD) = 190 0 : 2 = 95 0
⇒ ∠ (BCD) = ∠ (BAD) = 95 0