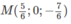Trong không gian Oxyz, hãy tìm trên mặt phẳng (Oxz) một điểm M cách đều ba điểm A(1; 1; 1), B(-1; 1; 0), C(3; 1; -1).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Phương trình của hai mặt phẳng (Oxy) và (Oxz) lần lượt là z = 0 và y = 0.
Điểm M(x ;y ;z) cách đều hai mặt phẳng đó khi và chỉ khi
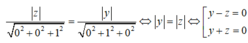

Đáp án B.
Rõ ràng A và B đều nằm về cùng một phía đối với mặt phẳng O x z (do đều có tung độ dương). Gọi A' là điểm đối xứng của A qua O x z thì A ' = − 1 ; − 3 ; 4 . Ta có M A + M B = M A ' + M B (do M ∈ O x z và A' là điểm đối xứng của A qua O x z ). Do đó M A + M B ngắn nhất ⇔ M A ' + M B ngắn nhất ⇔ A ' , M , N thằng hàng, tức M là giao điểm của A'B và O x z .
Ta có A ' B → = 4 ; 4 ; − 4 . Suy ra phương trình đường thẳng A ' B : x = 3 + t y = 1 + t z = − t .
Phương trình mặt phẳng ( O x z ) là y=0. Giải phương trình 1 + t = 0 ⇔ t = − 1 .
Suy ra M = 2 ; 0 ; 1 . Do đó M có hoành độ bằng 2. Vậy B là đáp án đúng.

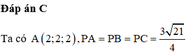
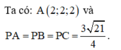
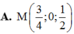

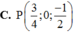
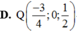
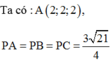

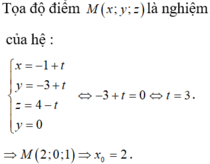

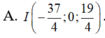
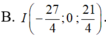
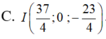
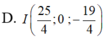
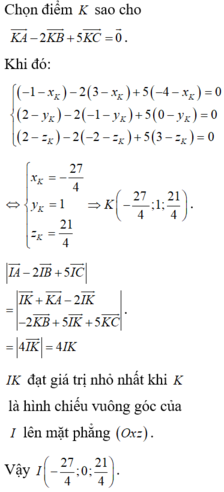
Điểm M thuộc mặt phẳng (Oxz) có tọa độ là (x; 0; z), cần phải tìm x và z. Ta có:
MA 2 = 1 - x 2 + 1 + 1 - z 2
MB 2 = - 1 - x 2 + 1 + z 2
MC 2 = 3 - x 2 + 1 + - 1 - z 2
Theo giả thiết M cách đều ba điểm A, B, C nên ta có MA 2 = MB 2 = MC 2
Từ đó ta tính được