Cho tám giác ABC vuông tại A , đường cao AH chia cạnh huyền thành hai đoạn BH = 4cm và Hc = 9cm
a) tính AH,AB,AC
b) Từ H kẻ vuông góc với Ab , HF vuông góc với AC ( E thuộc AB , F thuộc AC). Chứng mình rằng AB.AE=AF.AC và tam giác AEF đồng dạng với tam giác AC
c)Gọi D là trung điểm BC. Chúng minh rằng 2.sin ²C+cos ADB=1
giúp em với ạ


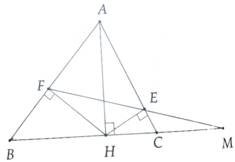
b: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)