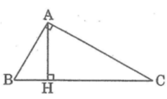
đảo trường sa lớn có dạng hình một tam giác vuông , cạnh huyền nằm theo hương đông bắc tây nam .Đường cao ứng với cạnh huyền chia tam giác này thành 2 phần có diện tích bằng 54000 m^2 và 96000 m^2 tính độ dài cạch huyền của tam giác vuông này
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử tam giác ABC vuông tại A và đường cao AH chia tam giác thành 2 phần có diện tích là \(54cm^2\) và \(96cm^2\).
Giả sử \(S_{AHB}=54cm^2,S_{AHC}=96cm^2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{2}.AH.HB=54\\\dfrac{1}{2}.AH.HC=96\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AH.HB=108\\AH.HC=192\end{matrix}\right.\)
\(\Rightarrow AH^2.HB.HC=20736\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH^2=HB.HC\)
\(\Rightarrow AH^2.HB.HC=AH^2.AH^2=AH^4=20736\Rightarrow AH=12\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}HB=\dfrac{108}{12}=9\\HC=\dfrac{192}{12}=16\end{matrix}\right.\Rightarrow BC=HB+HC=9+16=25\left(cm\right)\)

có S AHB = AH.HB/2 = 54 (gt) => AH.HB = 108
S AHC = AH.HC/2 = 96 (gt) => AH.HC = 192
=> AH^2.HB.HC = 108.192 = 20736 (1)
tg ABC có ^A = 90 (gt) ; AH _|_ BC => AH^2 = HB.HC (đl)
=> AH^4 = AH^2.HB.HC và (1)
=> AH^4 = 20736
=> AH = 12 do AH > 0
có AH.HB = 108 => HB = 9
AH.HC = 192 => HC = 16
=> HB + HC = 9 + 16 = 25

Gọi độ dài hình chiếu thứ nhất là x
=>Độ dài hình chiếu thứ 2 là x+14
Theo đề, ta có: x^2+14x=24^2=576
=>x^2+14x-576=0
=>x=18
=>Độ dai cạnh huyền là 18+18+14=50cm
\(a=\sqrt{18\cdot50}=30\left(cm\right)\)
\(b=\sqrt{32\cdot50}=40\left(cm\right)\)
S=1/2*30*40=15*40=600cm2

Gọi độ dài đoạn thẳng ngắn hơn được chia trên cạnh huyền là x (cm) với x>0
\(\Rightarrow\) Độ dài đoạn còn lại là \(x+14\)
Áp dụng hệ thức lượng trong tam giác vuông:
\(24^2=x\left(x+14\right)\)
\(\Leftrightarrow x^2+14x-576=0\Rightarrow\left[{}\begin{matrix}x=18\\x=-32\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\) Độ dài cạnh huyền là: \(18+\left(18+14\right)=50\left(cm\right)\)
Diện tích tam giác: \(S=\dfrac{1}{2}.24.50=600\left(cm^2\right)\)

Bài 1:
Áp dụng đl pytago ta có:
\(\left(y+z\right)^2=3^2+4^2=9+16=25\)
=> y + z = 5
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(3^2=y\left(y+z\right)=5y\)
=>\(y=\frac{3^2}{5}=1,8\)
Có: y + z =5
=>z=5-y=5-1,8=3,2
Áp dụng hên thức liên quan tới đường cao:
\(x^2=y\cdot z=1,8\cdot3,2=\frac{144}{25}\)
=>\(x=\frac{12}{5}\)

Giả sử tam giác ABC có góc (BAC) = 90 ° , AH ⊥ BC, BC = 5, AH = 2 và BH < CH
Ta có: BH + CH = 5 (1)
Theo hệ thức liên hệ giữa đường cao và cạnh huyền trong tam giác, ta có:
BH.CH = A H 2 = 2 2 = 4 (2)
Từ (1) và (2) suy ra: BH = 1 và CH = 4
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A B 2 = BH.BC = 1.5 = 5
Suy ra: AB = 5

Goi 2 canh goc vuong la b va c (b > c)
Ap dung he thuc luong va dinh ly Pythagore ta co he pt :
{ b.c = 5.2 = 10 (1)
{ b^2 + c^2 = 5^2 = 25 (2)
(1) ---> 2bc = 20 (3)
(2) + (3) ---> (b+c)^2 = 45 ---> b+c = 3 can 5 (4)
(2) - (3) ---> (b-c)^2 = 5 ---> b-c = can 5 (5)
(4),(5) ---> b = 2 can 5 ; c = can 5
Vay canh nho nhat cua tam giac vuong do la can 5.