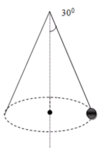
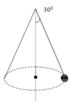
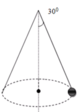
Một hòn đá được treo vào một điểm cố định bằng một sợi dây dài 1,00 m. Quay dây sao cho chất điểm chuyển động tròn đều trong mặt phẳng nằm ngang và thực hiện được 30 vòng trong một phút (H.II.2). Lấy g = 9,8 m/ s 2 . Tính góc nghiêng của dây so với phương thẳng đứng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khi dây đứt, hòn đá chuyển động như một vật bị ném ngang với vận tốc
v = ω r = ω lsin α = 3,14.1,00. 0,1167 = 0,366 m/s
Thời gian từ khi hòn đá bị văng ra đến khi chạm đất
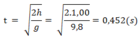
s = vt = 0,366.0,452 = 0,165 m = 16,5 cm.

Đáp án: A
Ta có:
![]()
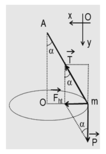
Chiếu lên phương ngang, chiều dương hướng về tâm của quỹ đạo:
Fht = mw2r = mw2lsina = Tsina
→ mw2l = T (1)
Ở đây w = 30 vòng/ph = 0,5 vòng/s = p rad/s.
Chiếu lên phương thẳng đứng, chiều dương hướng xuống:
0 = P - Tcosa = mg - Tcosa

Từ (2) và (1)
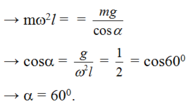
Sức căng sợi dây:
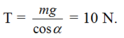

Ta có: \(F_{ht}=mg+T\)
\(\Leftrightarrow T^2=\left(mg\right)^2+F_{ht}^2\left(Pytago\right)\)
\(\Leftrightarrow T^2=F_{ht}^2+\left(mg\right)^2=\left(\dfrac{mv^2}{R}\right)+\left(mg\right)^2\)
\(\Rightarrow m=\dfrac{T}{\sqrt{g^2+\dfrac{v^4}{R^2}}}\approx0,8\left(kg\right)\)

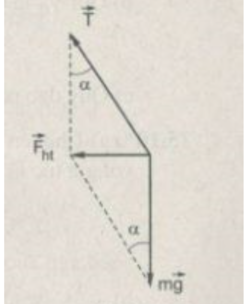
Từ hình vẽ ta có
F h t = mgtanα
Mà F h t = m v 2 /r = m v 2 /1.sin α
Suy ra m v 2 /1.sin α = mgtan α
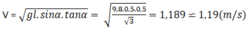

Chọn A.
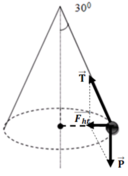
Tổng hợp lực của trọng lực và lực căng dây đóng vai trò là lực hướng tâm:
→ Fht/P = tan 30 o
→ Fht = 0,5.9,8. tan 30 o = 2,83 N
Quả cầu chuyển động theo quỹ đạo tròn với bán kính:
r = l sin 30 o ° = 0,5. sin 30 o ° = 0,25 m.
Mặt khác:
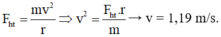

Đáp án A
Tổng hợp lực của trọng lực và lực căng dây đóng vai trò là lực hướng tâm.

Quả cầu chuyển động theo quỹ đạo tròn với bán kính
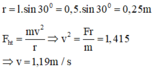

Chọn A.
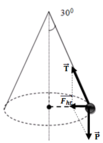
Tổng hợp lực của trọng lực và lực căng dây đóng vai trò là lực hướng tâm:
→ Fht/P = tan30o → Fht = 0,5.9,8.tan30o = 2,83 N
Quả cầu chuyển động theo quỹ đạo tròn với bán kính:
r = ℓsin30o = 0,5.sin30o = 0,25 m.
Mặt khác: → v = 1,19 m/s.
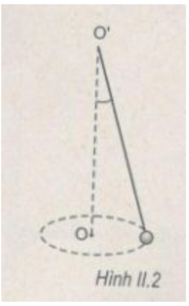
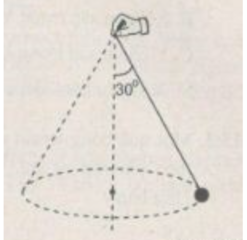
ω = 2 π f = 6,28.30/60 = 3,14(rad/s)
tan α = F h t /P = m ω 2 r/mg = ω .l.sin α /g
cos α = g/ ω 2 l = 9,8/( 3 , 14 2 .1,00) = 0,9940
α ≈ 6 ° 40 '