Xác định tọa độ giao điểm của parabol y = ax2 + bx + c với trục tung. Tìm điều kiện để parabol này cắt trục hoành tại hai điểm phân biệt, tại mỗi điểm và viết tọa độ của các giao điểm trong mỗi trường hợp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
5 tháng 6 2017
Điều kiện để (P): \(y=ax^2+bx+c\) cắt trục hoành tại hai điểm phân biệt là \(\Delta>0\).
Gọi \(x_1;x_2\) là hoành độ của hai giao điểm. Ta có:
\(x_{1,2}=\dfrac{-b\pm\sqrt{\Delta}}{2a}\);
Tọa độ giao điểm là:
\(A\left(\dfrac{-b+\sqrt{\Delta}}{2a};0\right)\); \(A\left(\dfrac{-b-\sqrt{\Delta}}{2a};0\right)\).
CM
18 tháng 3 2017
y = x2 – 2x có a = 1 ; b = –2 ; c = 0 ; Δ= b2 – 4ac = 4.
+ Đỉnh của Parabol là (1 ; –1).
+ Khi x = 0 thì y = 0. Vậy giao điểm với trục tung là O(0 ; 0).
+ Khi y = 0 thì x2 – 2x = 0. Phương trình có hai nghiệm x = 0 hoặc x = 2.
Vậy Parabol cắt trục hoành tại hai điểm O(0 ; 0) và A(2 ; 0).
CM
30 tháng 1 2019
y = –x2 + 4 có a = –1 ; b = 0 ; c = 4 ; Δ= b2 – 4ac = 0 – 4.( –1).4 = 16.
+ Đỉnh của Parabol là (0 ; 4).
+ Khi x = 0 thì y = 4. Vậy giao điểm với trục tung là A(0 ; 4).
+ Khi y = 0 thì –x2 + 4 = 0. Phương trình có hai nghiệm x = 2 hoặc x = –2.
Vậy Parabol cắt trục hoành tại hai điểm B(2 ; 0) hoặc C(–2 ;0).
CM
24 tháng 3 2017
y = –2x2 + 4x – 3 có a = –2 ; b = 4 ; c = –3 ; Δ= b2 – 4ac = 42 – 4.( –3).( –2) = –8
+ Đỉnh của Parabol là (1 ; –1).
+ Khi x = 0 thì y = –3. Vậy giao điểm với trục tung là A(0 ; –3).
+ Khi y = 0 thì –2x2 + 4x – 3 = 0. Phương trình vô nghiệm.
Vậy Parabol không cắt trục hoành.
CM
26 tháng 8 2018
y = x2 – 3x + 2 có a = 1 ; b = –3 ; c = 2 ; Δ = b2 – 4ac = (–3)2 – 4.2.1 = 1.
+ Đỉnh của Parabol là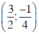 
+ Khi x = 0 thì y = 2. Vậy giao điểm với trục tung là A(0 ; 2).
+ Khi y = 0 thì x2 – 3x + 2 = 0. Phương trình có hai nghiệm x = 2 hoặc x = 1.
Vậy giao điểm với trục hoành là B(2 ; 0) và C(1 ; 0).
CM
20 tháng 12 2019
Ở đây a = 2; b = -2; c = -2. Ta có Δ = ( - 1 ) 2 - 4 . 2 . ( - 2 ) = 17
Trục đối xứng là đường thẳng x = 1/4; đỉnh I(1/4; -17/8) giao với trục tung tại điểm (0; -2).
Để tìm giao điểm với trục hoành ta giải phương trình
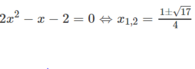
Vậy các giao điểm với trục hoành là
CM
26 tháng 6 2019
Trục đối xứng x = -1/4; đỉnh I(-1/4; -17/8) giao với trục tung tại điểm (0;2); giao với trục hoành tại các điểm
19 tháng 4 2023
1: Tọa độ A là:
y=0 và 4x+m-3=0
=>x=(-m+3)/4 và y=0
=>OA=|m-3|/4
Tọa độ B là:
x=0 và y=m-3
=>OB=|m-3|
Theo đề, ta có: 1/2*(m-3)^2/4=9
=>(m-3)^2/4=18
=>(m-3)^2=72
=>\(m=\pm6\sqrt{2}+3\)
2:
PTHĐGĐ là:
x^2-4x-m+3=0
Δ=(-4)^2-4*(-m+3)=16+4m-12=4m+4
Để (P) cắt (d) tại hai điểm phân biệt thì 4m+4>0
=>m>-1
(4-x1)(x2-1)=2
=>4x2-4-x1x2+1=2
=>x2(x1+x2)-3-(-m+3)=2
=>x2*4-3+m-3=2
=>x2*4=2-m+6=8-m
=>x2=2-1/2m
=>x1=4-2+1/2m=1/2m+2
x1*x2=-m+3
=>-m+3=(1/2m+2)(2-1/2m)=4-1/4m^2
=>-m+3-4+1/4m^2=0
=>1/4m^2-m-1=0
=>m^2-4m-4=0
=>\(m=2\pm2\sqrt{2}\)
+ Giao điểm của parabol với trục tung:
Tại x = 0 thì y = a.02 + b.0 + c = c.
Vậy giao điểm của parabol với trục tung là A(0 ; c).
+ Giao điểm của parabol với trục hoành :
Tại y = 0 thì ax2 + bx + c = 0 (*).
Để parabol cắt trục hoành tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt ⇔ Δ = b2 – 4ac > 0.
Khi Δ > 0 thì phương trình (*) có hai nghiệm là
Tọa độ hai giao điểm là