Trên đường tròn lượng giác cho điểm M xác định bởi sđ cung AM = α (0 < α < π/2). Gọi M1, M2, M3 lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc tọa độ. Tìm số đo các cung AM1, AM2, AM3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

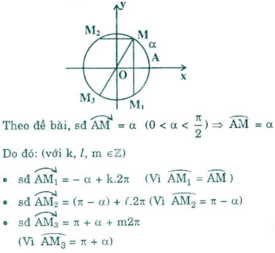

-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B

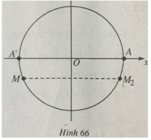
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
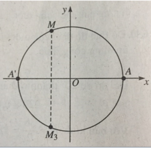
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D

Cách 1. Suy luận.
Điểm M nằm ở góc phần tư thứ IV nên điểm M 1 nằm ở góc phần tư thứ hai. Số đo A M 1 dương nên hai phương án A, D bị loại. Mặt khác sđ A M 1 < 180 o nên phương án B bị loại.
Vậy đáp án là C.
Cách 2. Tính trực tiếp.
Gọi B là giao điểm của đường phân giác góc xOy với đường tròn. Ta có
Sđ A B = 45 o , s đ M A = 70 o
Suy ra sđ MB = 115 o .
Mà sđ B M 1 = sđ MB nên sđ A M 1 = 45 o + 115 o = 160 o .
Đáp án: C

a) a = c, b = - d
b) a = -c, b = d
c) a = d, b = c
d) a = -c, b = - d

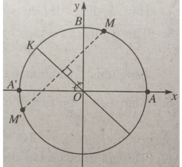
Sđ MK = sđ KM’ = 55 o
⇒ sđ AM’ = sđ AM + sđ MK + sđ KM’ = 190 o .
Đáp án: C
