Cho tam giác ABC vuông tại A, phân giác BD. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh rằng: BD là đường thẳng trung trực của AE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 8 2017
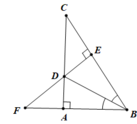
b. Ta có AB = BE ⇒ B nằm trên đường trung trực của AE (0.5 điểm)
Do ∆ABD = ∆EBD nên AD = DE (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AE
Vậy BD là đường trung trực của AE (0.5 điểm)
30 tháng 4 2022
a: XétΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE và DA=DE
hay BD là đường trung trực của AE
b: Ta có: AD=DE
mà DE<DC
nên AD<CD
18 tháng 6 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: BA=BE
DA=DE
=>BD là trung trực của AE
19 tháng 6 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: BA=BE
DA=DE
=>BD là trung trực của AE
c: Xét ΔBFC có
FE,CA là đường cao
FE cắt CA tại D
=>D là trực tâm
=>BD vuông góc FC
25 tháng 3 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
c: ΔBFC can tai B
mà BD là phân giác
nên BD là trung tuyến
10 tháng 8 2015
Bài này không khó, cần thì mình giải cho bạn nhưng mà phần b bạn sai đề
11 tháng 2 2020
a) Ta xét t/g ABD vuông tại a và kẻ DE vuông góc với BC có:
=>BD sẽ là cạnh chung
=>ADB=BDE (BD là tia phân giác của ABE)
=>T/gABD=t/gEDB (cạnh huyền-góc nhọn)
=>AB=EB (2 cạnh tương ứng)
=>B thuộc đường trung trực của AE
=>AD=ED (2 cạnh tương ứng)
=>D thuộc đường trung trực của AE
=>BD là đường trung trực của AE
b) Xét t/g AFD và t/gECD ta có:
=>FAD=CED=90o
=>AD=ED(t/gABD=t/gEDB)
=>ADF=EDC (2 góc đối đỉnh)
=>T/gDAF=t/gEDC (c.g.c)
=>DF=DC ( 2 cạnh tương ứng)
c)
Vì t/gADF vuông tại A nên ta có:
AD<FD (quan hệ giữa các cạnh góc đối diện nhau trong 1 t/g vuông)
=>FD=CD
=>AD<DC
=> (đpcm).
Xét ΔABD và ΔEBD có:
BD chung
∠ABD = ∠EBD ( do BD ,là tia phân giác của góc ABC )
∠BAD = ∠BED = 90º
Suy ra: ΔABD = ΔEBD (cạnh huyền – góc nhọn) ⇒ BA = BE, DA = DE.
Do BA = BE nên B thuộc đường trung trực của AE.
Do DA = DE nên D thuộc đường trung trực của AE.
Do đó BD là đường trung trực của AE.