Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC vuông tại B. Trong mp(SAB), kẻ AM vuông góc với SB tại M. Trên cạnh SC lấy điểm N sao cho SM/SB = SN/SC .
Chứng minh rằng:
a) BC ⊥ (SAB), AM ⊥ (SBC)
b) SB ⊥ AN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

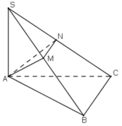


Trong mặt phẳng (SBC), nối HM kéo dài cắt BC tại K \(\Rightarrow AK\in\left(ABC\right)\)
Từ câu a có \(AM\perp\left(SBC\right)\) \(\Rightarrow AM\perp SC\)
Mà \(SC\perp AH\Rightarrow SC\perp\left(AHM\right)\Rightarrow SC\perp AK\) (1)
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AK\) (2)
(1);(2) \(\Rightarrow AK\perp\left(SAC\right)\Rightarrow AK\perp AC\)

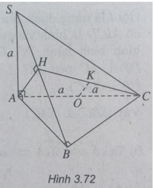
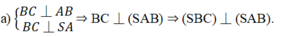
b) AH ⊥ SB mà SB là giao tuyến của hai mặt phẳng vuông góc là (SBC) và (SAB) nên AH ⊥ (SBC).
c) Xét tam giác vuông SAB với đường cao AH ta có:
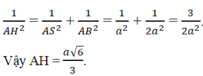
d) Vì OK ⊥ (SBC) mà AH ⊥ (SBC) nên OK // AH, ta có K thuộc CH.
OK = AH/2 = (a√6)/6.

\(BC=AB\sqrt{2}=a\sqrt{2}\)
\(SB=\sqrt{SC^2+BC^2}=a\sqrt{3}\) ; \(SA=\sqrt{SC^2+AC^2}=a\sqrt{2}\)
\(V_{SBAC}=\dfrac{1}{3}SC.\dfrac{1}{2}AB^2=\dfrac{a^3}{6}\)
\(\dfrac{V_{SCEF}}{V_{SABC}}=\dfrac{SF}{SB}.\dfrac{SE}{SA}=\left(\dfrac{SC}{SB}\right)^2\left(\dfrac{SC}{SA}\right)^2=\left(\dfrac{a}{a\sqrt{3}}\right)^2.\left(\dfrac{a}{a\sqrt{2}}\right)^2=\dfrac{1}{6}\)
\(\Rightarrow V_{SCEF}=\dfrac{1}{6}.\dfrac{a^3}{6}=\dfrac{a^3}{36}\)
Kết quả không có a³/18
Chỉ có là A)a³/6. B)a³/16
C)a³/26. D)a³/36 thôi ạ