Giải các phương trình sau trên tập số phức:
a) (1 + 2i)x – (4 – 5i) = –7 + 3i
b) (3 + 2i)x – 6ix = (1 – 2i)[x – (1 + 5i)]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
31 tháng 7 2018
a) đặc : \(x=a+bi\) với \(a;b\in R\) và \(i^2=-1\)
ta có : \(\left(1+2i\right)x-4\left(4-5i\right)=-7+3i\)
\(\Leftrightarrow\left(1+2i\right)\left(a+bi\right)-4\left(4-5i\right)=-7+3i\)
\(\Leftrightarrow a-2b+2ai+bi-16+20i=-7+3i\)
\(\Leftrightarrow\left(a-2b-16\right)+\left(2a+b+20\right)i=-7+3i\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-2b-16=-7\\2a+b+20=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a-2b=9\\2a+b=-17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-5\\b=-7\end{matrix}\right.\) vậy \(x=-5-7i\)
câu b lm tương tự nha .
PT
1
AH
Akai Haruma
Giáo viên
30 tháng 5 2021
Lời giải:
a)
$(3-2i)x+(5-7i)y=1-3i$
$\Leftrightarrow (3x+5y)-(2x+7y)i=1-3i$
\(\Leftrightarrow \left\{\begin{matrix}
3x+5y=1\\
2x+7y=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x=\frac{-8}{11}\\
y=\frac{7}{11}\end{matrix}\right.\)
b)
\((1+2i)^2x-(4-5i)y=2i\)
\(\Leftrightarrow (-3+4i)x-(4-5i)y=2i\)
\(\Leftrightarrow -(3x+4y)+(4x+5y)i=2i\Leftrightarrow \left\{\begin{matrix} -(3x+4y)=2\\ 4x+5y=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x=10\\ y=-8\end{matrix}\right.\)
PT
1
CM
20 tháng 6 2017
(3 + 2i).z - (4 + 7i) = 2 – 5i
⇔ (3 + 2i).z = (2 – 5i) + (4 + 7i)
⇔ (3 + 2i).z = 6 + 2i
PT
1
CM
14 tháng 8 2018
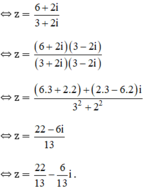
(3 - 2i)z + (4 + 5i) = 7 + 3i
⇔ (3 – 2i).z = (7 + 3i) – (4 + 5i)
⇔ (3 – 2i).z = 3 – 2i
⇔ z = 1.
PT
1
1 tháng 4 2017
a) Ta có (3 - 2i)z + (4 + 5i) = 7 + 3i <=> (3 - 2i)z = 7 + 3i - 4 - 5i
<=> z = <=> z = 1. Vậy z = 1.
b) Ta có (1 + 3i)z - (2 + 5i) = (2 + i)z <=> (1 + 3i)z -(2 + i)z = (2 + 5i)
<=> (1 + 3i - 2 - i)z = 2 + 5i <=> (-1 + 2i)z = 2 + 5i
z =
Vậy z =
c) Ta có + (2 - 3i) = 5 - 2i <=>
= 5 - 2i - 2 + 3i
<=> z = (3 + i)(4 - 3i) <=> z = 12 + 3 + (-9 + 4)i <=> z = 15 -5i
a) (1 + 2i)x = − 3 −2i
b) (2 − 2i)x = −(11 + 3i)