Cho biết (4m+5)chia hết cho 23.Chứng minh rằng (7m+3)chia hết cho 23
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 7 2019
a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:
10 tháng 10 2021
4₁ A= 2 +2²³ +2 ² + + 220
a₁ A = 2₁ [1 + 2 +2²¹ +. +2¹2):2 Vay A chia hết choi
b₁ A = 2 + 2² +2²+ + 220 (2 +2²) + (2 ² + 2 9) + . + (219+220)
= 2₁ (1 + 2) + 2² (2+1). .. +2 19 (2+1) + = 2₁3 + 2³.3 + ..+ 219.3.
= (2+2 ³+ + 219) 3:3 Vậy A chia hết cho 3 A = 2 + 2 ² + 2³ + 2ª +. 20 + 2.9+ +2
2+2 ³ + 2² +2²4 + + 218 + 720 +2²³ +2²+ +218 +220 2. (2 +2²) + 2² (1+2²) +.. + 218 ( 1 +2²) = 2 5 +2²5 + + 218 5. 12 +2° + 2 ... +218 ) 5 : 5.
vậy A chia hết cho 5
VD
14 tháng 7 2018
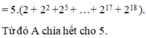
7)a) abcabc : abc = 1001
abcabc = 1001 x abc . Mà 1001 chia hết cho 7; 11; 13 nên 1001 x abc chia hết cho 7; 11; 13 . Vậy abcabc chia hết cho 7; 11; 13 ( đpcm)
b .Vì abc = 2 . deg nên abcdeg : deg = 2001
abcdeg = 2001 x deg. Do 2001 chia hết cho 23 và 29 nên 2001 x deg chia hết cho 23 và 29 . Vậy abcdeg chia hết cho 23 và 29 ( đpcm)
5 tháng 11 2018
Ta có :
abcabc = 1000abc + abc
= 1001 . abc
= 7 . 11 . 13 . abc chia hết cho 7 ; 11 ; 13
DD
1
21 tháng 9 2020
+, Ta có:
\(B=23!+19!-15!\)
\(B=\left(1\times2\times...\times11\times...\times23\right)+\left(1\times2\times...\times11\times...\times19\right)-\left(1\times2\times...\times11\times...\times15\right)\)
\(B=11\times\left[\left(1\times2\times...\times10\times12\times...\times23\right)+\left(1\times2\times...\times10\times12\times...\times19\right)-\left(1\times2\times...\times10\times12\times...\times15\right)\right]\)
\(\Rightarrow B⋮11\)
+, Ta có:
\(B=23!+19!-15!\)
\(B=\left(1\times2\times...\times10\times11\times...\times23\right)+\left(1\times2\times...\times10\times11\times...\times19\right)-\left(1\times2\times...\times10\times11\times...\times15\right)\)
\(B=11\times10\times\left[\left(1\times2\times...\times9\times12\times...\times23\right)+\left(1\times2\times...\times9\times12\times...\times19\right)-\left(1\times2\times...\times9\times12\times...\times15\right)\right]\)
\(B=110\times\left[\left(1\times2\times...\times9\times12\times...\times23\right)+\left(1\times2\times...\times9\times12\times...\times19\right)-\left(1\times2\times...\times9\times12\times...\times15\right)\right]\)
\(\Rightarrow B⋮110\)
+,Ta có:
\(B=23!+19!-15!\)
\(B=\left(1\times2\times...\times5\times...\times23\right)+\left(1\times2\times...\times5\times...\times19\right)-\left(1\times2\times...\times5\times...\times15\right)\)
\(B=5\times\left[\left(1\times2\times...\times4\times6\times...\times23\right)+\left(1\times2\times...\times4\times6\times...\times19\right)-\left(1\times2\times...\times4\times6\times...\times15\right)\right]\)
\(\Rightarrow B⋮5\)
~ Chúc bạn học tốt ~!
T
1
6 tháng 10 2020
Ta có: 7a+3b⋮23⇒6(7a+3b)⋮237a+3b⋮23⇒6(7a+3b)⋮23
⇒6(7a+3b)+(4a+5b)⋮23⇒6(7a+3b)+(4a+5b)⋮23
⇒46a+23b⋮23⇒23(2a+b)⋮23⇒46a+23b⋮23⇒23(2a+b)⋮23(Đúng)
Vậy 4a+5b⋮23
Ta gọi 4m+5 là a;7m+3 là b,ta có:
a chia hết cho 23 thì 4a cũng chia hết cho 23 nên 4a=(4m+5)=16m+20
Ta đặt c=4a+b=(16m+20)+(7m+3)=(16+7)m+(20+3)=23m+23
Vì 23m+23 luôn chia hết cho 23 mà 16m+20 cũng chia hết nên 7m+3 phải chia hết cho 23