Trên hình 12.1 SGK, đồ thị hình sin của i cắt:
trục hoành tại những điểm có tọa độ bằng bao nhiêu T?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trên hình 12.1 SGK, đồ thị hình sin của i cắt:
trục hoành tại những điểm có tọa độ bằng bao nhiêu T?


Đồ thị cắt trục tung tại điểm có giá trị i bằng bao nhiêu Im
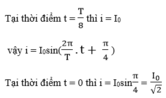

Đáp án D
Ta có: y ' = 3 a x 2 + 2 b x + c
+) Đồ thị hàm số f'(x) đi qua gốc tọa độ => c=0
+) Đồ thị hàm số f'(x) có điểm cực trị:
1 ; − 1 ⇒ 6 a + 2 b = 0 3 a + 2 b = − 1 ⇔ a = 1 3 b = − 1
Vậy hàm số f ' x = x 2 − 2 x . Đồ thị hàm số f(x) tiếp xúc với trục hoành nên có cực trị nằm trên trục hoành. Các giá trị cực trị của hàm số f(x) là:
f 0 = d f 2 = 8 3 − 4 + d = − 4 3 + d
do điểm tiếp xúc có hoành độ dương
=> d = 4 3 => f(x) cắt trục tung tại điểm có tung độ 4 3

Đáp án C.
Dễ thấy trên đoạn − 3 ; 0 thì f x ≥ 0 , trên đoạn 0 ; 4 thì f x ≤ 0 .
S = ∫ − 3 4 f x d x = ∫ − 3 0 f x d x + ∫ 0 4 f x d x = ∫ − 3 0 f x d x − ∫ 0 4 f x d x
= ∫ − 3 0 f x d x + ∫ 4 0 f x d x
.

1: Để hàm số đồng biến thì m-3>0
hay m>3
2: Thay x=0 và y=0 vào (d), ta được:
3m+7=0
hay \(m=-\dfrac{7}{3}\)
Đồ thị hình sin cắt trục hoành tại những điểm có giá trị