Có bốn học sinh đứng ở bốn vị trí quanh một cái tủ đứng như trong hình 9.2. Hãy chỉ ra những cặp học sinh có thể nhìn thấy nhau. Đánh dấu vào bảng sau đây những cặp đó.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những cặp học sinh nhìn hấy nhau là:
An thấy : Thanh, Hải
Thanh thấy: An, Hải
Hải thấy: An, Thanh, Hà
Hà thấy: Hải
Có những bạn không nhìn thấy nhau bởi vì đã bị tủ đứng che khuất tầm mắt nên ánh sáng không thể truyền vào mắt theo đg vòng từ bạn -> mắt

| Tên tác phẩm | Thể loại | Cốt truyện | Nhân vật | Nhân vật kể chuyện |
|---|---|---|---|---|
| Dế Mèn phiêu lưu kí | Truyện dài | + | + | + |
| Sông nước Cà Mau | Truyện dài | + | + | + |
| Vượt thác | Truyện dài | + | + | + |
| Buổi học cuối cùng | Truyện dài | + | + | + |
| Cô Tô | Kí | + | ||
| Cây tre Việt Nam | Kí | + | + | |
| Lòng yêu nước | Kí | |||
| Lao xao | Kí | + |
Nhận xét:
+ Giống: Truyện ngắn và kí đều là những câu chuyện có người kể chuyện.
+ Khác: Truyện thường có đầy đủ nhân vật, cốt truyện còn thể kí có thể có hoặc không có nhân vật, cốt truyện.

Chọn D
Xếp ngẫu nhiên tám học sinh thành hàng ngang, có 8! cách. Suy ra n ( Ω ) = 8! = 40320
Gọi A là biến cố cần tính xác suất.
Ta coi Hoàng, Lan, Nam ( Lan ở giữa) là một nhóm. Khi đó vì hai bên nhóm này bắt buộc là nữ nên coi nhóm này là một nam. Vậy có thể coi ta có ba nam và ba nữ.
Khi đó có hai trường hợp xảy ra.
Trường hợp 1: Nam ngồi vị trí lẻ.
Xếp ba nam vào vị trí lẻ có 3! cách.
Xếp ba nữ vào vị trí chẵn có 3! cách.
Hoán vị hai học sinh nam trong nhóm ( Hoàng- Lan- Nam) có 2! cách.
Vậy số cách sắp xếp trong trường hợp này là 3!.3!.2! = 72 cách.
Trường hợp 2: Nam ngồi vị trí chẵn.
Tương tự trường hợp này có 3!.3!.2! = 72 cách.
Suy ra n(A) = 72 + 72 = 144 cách.
Vậy 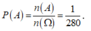

Chọn A.
Cơ thể dị hợp 4 cặp gen có kiểu gen ( Aa, Ee, Bb, Dd).
Vì hoán vị chỉ ở cặp Aa nên BD = bd = 0,5.
AE BD = 17,5%
=> AE = ae = 0,175 : 0,5 = 35%
=> Ae = aE = 15%
% Ae BD = 15% x 0,5 = 7,5%
aE bd = 15% x 0,5 = 7,5%
ae BD = 35% x 0,5 = 17.5%
AE Bd không tồn tại do chỉ có hoán vị ở cặp Aa.

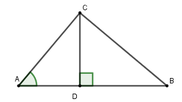
Độ cao của máy bay là CD, độ dài AB = 100m. Đào đứng ở A, Mai đứng ở B
Gọi AD = x (0 < x < 100) => BD = 150 – x
Xét ACD vuông tại D, ta có CD = AD.cot A = x . c o t 45 0 = x
Xét ABD vuông tại D, ta có CD = BD.cot B = (150 – x). c o t 35 0
Nên x = (150 – x). c o t 35 0 => x ≈ 88,22 (thỏa mãn)
=> CD = x = 88,22m
Vậy độ cao của diều lúc đó so với mặt đất là 88,22m
Đáp án cần chọn là: D

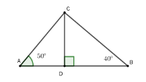
Độ cao của diều là CD, độ dài AB = 100m. Trung đứng ở A, Dũng đứng ở B
Gọi AD = x (0 < x < 100)
=> BD = 100 – x
Xét ACD vuông tại D, ta có CD = AD.tan A = x . tan 50 0
Xét ABD vuông tại D, ta có CD = BD.tan B = (100 – x). tan 40 0
Nên x . tan 50 0 = (100 – x). tan 40 0
![]()
Vậy độ cao của diều lúc đó so với mặt đất là 49,24m
Đáp án cần chọn là: B

Chọn D
Xếp ngẫu nhiên 8 học sinh có 8! cách.
"Buộc" Hoàng, Lan, Nam thành một nhóm. Khi đó vì hai bên nhóm này bắt buộc là nữ nên ta xem nhóm ba người này là một nam. Vậy có ba nam và ba nữ.
Trường hợp 1: nam ngồi vị trí lẻ.
Xếp 3 nam vào 3 vị trí lẻ: 3!
Xếp 3 nữ vào 3 vị trí chẵn: 3!
Hoán vị hai học sinh nam trong nhóm: 2!
Suy ra số cách xếp trong trường hợp này là: 3!.3!.2!=72 cách
Trường hợp 2: nam ngồi vị trí chẵn
Tương tự có 72 cách
Vậy có 72 + 72 = 144 cách xếp tám học sinh không có hai học sinh cùng giới đứng cạnh nhau, đồng thời Lan đứng cạnh Hoàng và Nam.
Suy ra xác suất cần tìm là P = 144 8 ! = 1 280 .
Vì tủ chắn sáng, và ánh sáng tuân theo định luật truyền thẳng nên ta chọn được kết quả sau:
Những cặp nhìn thấy nhau:
An – Thanh; An – Hải; Thanh – Hải; Hải – Hà.