Áp dụng quy tắc cộng đại số, hãy giải hệ (III) bằng cách trừ từng vế hai phương trình của (III).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


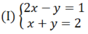
Trừ từng vế hai phương trình của hệ (I) ta được phương trình:
(2x – y) – (x + y) = 1 – 2 hay x – 2y = -1
Khi đó, ta thu được hệ phương trình mới:
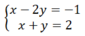
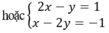

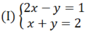
Trừ từng vế hai phương trình của hệ (I) ta được phương trình:
(2x – y) – (x + y) = 1 – 2 hay x – 2y = -1
Khi đó, ta thu được hệ phương trình mới:
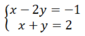
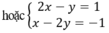

Ta có: 3x < 2x + 5 ⇔ 3x – 2x < 5 ⇔ x < 5
Vậy tập nghiệm của bất phương trình là: {x|x < 5}

Ta có: x + 3 > -6 ⇔ x > -6 – 3 ⇔ x > -9
Vậy tập nghiệm của bất phương trình là: {x|x > -9}

Ta có: x – 2 > 4 ⇔ x > 4 + 2 ⇔ x > 6
Vậy tập nghiệm của bất phương trình là: {x|x > 6}

Ta có: x – 4 < -8 ⇔ x < -8 + 4 ⇔ x < -4
Vậy tập nghiệm của bất phương trình là: {x|x < -4}

Lấy phương trình thứ nhất trừ đi phương trình thứ hai vế với vế, ta được: 5y = 5
Do đó
QUẢNG CÁOVậy hệ phương trình có nghiệm duy nhất (7/2;1)