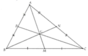
Cho tam giác ABC có ba đường trung tuyến AM,BN,CK cắt nhau tại G. So sánh SBGM và SCGM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 4 2017
a) Tam giác AGP và PGB có chung đường cao hạ từ đỉnh G và AP = PB nên SAGP = SPGB
Tương tự, ta có: SBGM = SMGC và SCGN = SNGA.
Vì G là trọng tâm DABC Þ AG = 2GM.
Þ SBGM = 1 2 SABG Þ SBGM = SAGP = SPGB.
Chứng minh tương tự, ta suy ra được:
SAGP = SPGB = SBGM = SMGC = SCGN = SNGA
b) Sử dụng kết quả câu a) ta có diện tích mỗi tam giác bằng 1 6 SABC, từ đó suy ra ĐPCM.
17 tháng 5 2022
vì tg ABC cân tại A
=> AM là đường phân giác
=>góc BAG = góc CAG (t/c đường phân giác )
xét tam giác ABG và tam giác AGC có
góc BAG = góc CAG (cmt)
AG : chung
AB = AC( gt )
=> tg AGB = tg AGC( C-G-C )
13 tháng 3 2022
a)Ta có: △ABC có 2 đường trung tuyến BI và CK giao nhau tại G
=> G là trọng tâm của tam giác ABC
=> AG là đường trung tuyến
Mà AG cắt BC tại M
=> AM là đường trung tuyến
=> MB= MC
Xét tam giác ABC có K là TĐ AB ; G là TĐ của AD
=> KG // BD
Mà C thuộc KG
=> GC // BD.=> B1 = C1( 2 góc so le trong)
Xét tam giác BMC và tam giác CMG có
MB = MC; M1 = M2; B1 = C1
=> △BMC = △CMG (g . c . g) (1)
Từ (1)=> BD=GC (2 cạnh t/ứ)
Có CG + KG = CK
=>CG < CK
Mà BD = CG
=> BD < CK
17 tháng 5 2022
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao và AM cũng là phân giác
Xét ΔABG và ΔACG có
AB=AC
\(\widehat{BAG}=\widehat{CAG}\)
AG chung
Do đó: ΔABG=ΔACG
b: Xét ΔBIC có
M là trung điểm của BC
MG//IC
Do đó: G là trung điểm của BI
Xét ΔBIC có
M là trung điểm của BC
G là trung điểm của BI
Do đó: MG là đường trung bình
=>MG=1/2CI
24 tháng 2 2022
1:
Xét ΔABC có
BI là trung tuyến
CK là trung tuyến
BI cắt CK tại G
Do đó: G là trọng tâm của ΔABC
mà M là giao điểm của AG và BC
=>AG=2/3MA và M là trung điểm của BC
=>AG=2GM
=>GD=2GM
=>M là trung điểm của GD
Xét ΔMBD và ΔMCG có
MB=MC
\(\widehat{BMD}=\widehat{CMG}\)
MD=MG
Do đó; ΔMBD=ΔMCG
2: Ta có: ΔMBD=ΔMCG
nên BD=CG
mà CG<CK
nên BD<CK
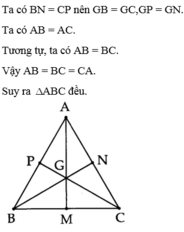
SBGM = SCGM