Cho tam giác ABC vuông ở A và đường cao AH.Vẽ đường tròn tam O đường kính AB.Biết BH = 2cm và HC = 6cm.Tính: Tổng diện tích hai hình viên phân AmH và BnH (ứng với các cung nhỏ)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 6 2018
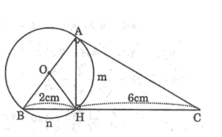
Ta có AB=4cm ⇒ OB =2cm
Tam giác OBH có OB = OH =HB = 2cm nên tam giác OBH đều
CM
24 tháng 4 2018
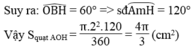
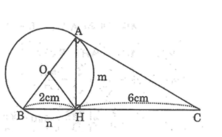
Trong tam giác ABC vuông tại A nên ta có:
A B 2 = BH.BC =2.(2+6)=2.8=16
suy ra AB = 4cm
Diện tích hình tròn tâm (O) là :
S=π. A B / 2 2 = π. 4 / 2 2 = 4π ( c m 2 )
10 tháng 5 2018
Bạn tự vẽ hình nha
a)Ta có góc BEH =90 độ (góc nội tiếp chắn nửa đường tròn)
và góc FHC = 90 độ (góc nội tiếp chắn nửa đường tròn)
Xét tứ giác AFHE , ta có:
góc EAF =90 độ (tam giác ABC vuông tại A)
góc AEH =90 độ (cmt)
góc AFH=90 độ (cmt)
=> tứ giác AFHE là hình chữ nhật (tứ giác có 3 góc vuông)
b)Gọi I là giao điểm của AH và EF
Ta có: AH=EF (hcn AFHE) (1)
mà 2 đường chéo AH và EF cắt nhau tại I (vẽ thêm)
=>I là trung điểm của AH và EF (2)
từ (1) và (2)=> IE=IH=IA=IF
Ta có: góc IHF =góc ACH (phụ với góc HAC)
mà góc IHF = góc IFH (tam giác IHF cân tại I (IH=IF) )
=>góc ACH = góc IFH (cùng = góc IHF)
mà góc IFH= góc AEF (2 góc so le trong của AE song song HF(cùng vuông góc AC))
=>góc AEF =góc ACH=>tứ giác BEFC nội tiếp đường tròn
c)Gọi J là tâm của nửa đường tròn đường kính BH
và K là tâm của nửa đường tròn đường kính HC
Ta có: tam giác KFC cân tại K (KF=KC)
=>góc KFC = góc KCF mà góc KCF=góc IFH (cmt)
=>góc KFC =góc IFH (cùng =góc KCF)
mà góc KFC + góc HFK =90 độ (góc HFC =90 độ)
=>góc IFH + góc HFK =90 độ => góc IFK =90 độ
=>EF là tiếp tuyến của nửa (K) (I thuộc EF) (3)
Ta lại có: tam giác JEH cân tại J (JE=JH)
=> góc JEH =góc JHE
mà góc JHE = góc HCF ( 2 góc so le trong của HE song song CA ( cùng vuông góc AB) )
và góc HCF = góc AEF (cmt)
=>góc JEH= góc AEF
mà góc AEF + góc HEF = 90 độ (góc HEA = 90 độ)
=>góc JEH + góc HEF =90 độ => góc JEF = 90 độ
=>EF là tiếp tuyến của nửa (J) (4)
Từ (3) và (4) => EF là tiếp tuyến chung 2 nửa dường tròn dường kính BH và HC
AA
Admin (a@olm.vn)
Admin
VIP
11 tháng 5 2017
a) \(MN^2=NH.NQ=2.\left(2+6\right)=16\)
=> MN = 4 (cm). => Bán kính hình tròn tâm O là MN/2 = 2 (cm)
=> Diện tích hình tròn tâm O là: 2.2.3,14 = ...12,56 (cm2)
b) Ta có tam giác ONH là tam giác đều (vì ON = OH = HN = 2).
Suy ra \(\widehat{NOH}=60^o\) => \(\widehat{MOH}=180^o-60^o=120^o\)
=> Diện tích quạt tròn MOH là: \(\frac{12,65}{360}.120=\frac{12,65}{3}\left(cm^2\right)\)
30 tháng 4 2023
a: góc BOC=2*góc A=90 độ
=>OB^2+OC^2=BC^2
=>2*R^2=2^2=4
=>R=căn 2
\(S_{\left(O\right)}=R^2\cdot pi=2pi\left(cm^2\right)\)
b: \(S_{q\left(BOC\right)}=pi\cdot2\cdot\dfrac{90}{360}=\dfrac{1}{2}\cdot pi\left(cm^2\right)\)
\(S_{BOC}=\dfrac{1}{2}\cdot OB\cdot OC=\dfrac{1}{2}\cdot2=1\)
=>\(S_{viênphân}=\dfrac{1}{2}\cdot3.14-1=0.57\left(cm^2\right)\)
CH
Cô Hoàng Huyền
Admin
VIP
29 tháng 12 2017
Câu hỏi của VRCT_Ran love shinichi - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
Trong tam giác vuông ABC có:
A H 2 = HB.HC =2.6=12
Suy ra: AH =2. 3 cm
Diện tích tam giác AHB:
Tổng diện tích hai hình viên phân AmH và BnH bằng diện tích nửa hình tròn tâm O đường kính AB trừ diện tích tam giác AHB có: