Giải các phương trình sau bằng cách biến đổi chúng thành những phương trình với vế trái là một bình phương còn vế phải là một hằng số. 3 x 2 – 6x + 5 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 3 2017
Ta có : x 2 – 6x + 5 = 0 ⇔ x 2 – 2.3x + 5 + 4 = 4
⇔ x 2 – 2.3x + 9 = 4 ⇔ x - 3 2 = 2 2
⇔ x – 3 = ± 2 ⇔ x – 3 = 2 hoặc x – 3 = -2
⇔ x = 1 hoặc x = 5
Vậy phương trình có hai nghiệm x 1 = 1, x 2 = 5
18 tháng 5 2022
a: \(\Leftrightarrow x^2-3x+\dfrac{9}{4}=\dfrac{5}{4}\)
=>(x-3/2)2=5/4
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{3}{2}=\dfrac{\sqrt{5}}{2}\\x-\dfrac{3}{2}=-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{5}+3}{2}\\x=\dfrac{-\sqrt{5}+3}{2}\end{matrix}\right.\)
b: \(x^2+\sqrt{2}x-1=0\)
nên \(x^2+2\cdot x\cdot\dfrac{\sqrt{2}}{2}+\dfrac{1}{2}=\dfrac{3}{2}\)
\(\Leftrightarrow\left(x+\dfrac{\sqrt{2}}{2}\right)^2=\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{6}}{2}\\x+\dfrac{\sqrt{2}}{2}=-\dfrac{\sqrt{6}}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{6}-\sqrt{2}}{2}\\x=\dfrac{-\sqrt{6}-\sqrt{2}}{2}\end{matrix}\right.\)
c: \(5x^2-7x+1=0\)
\(\Leftrightarrow x^2-\dfrac{7}{5}x+\dfrac{1}{5}=0\)
\(\Leftrightarrow x^2-2\cdot x\cdot\dfrac{7}{10}+\dfrac{49}{100}=\dfrac{29}{100}\)
\(\Leftrightarrow\left(x-\dfrac{7}{10}\right)^2=\dfrac{29}{100}\)
hay \(x\in\left\{\dfrac{\sqrt{29}+7}{10};\dfrac{-\sqrt{29}+7}{10}\right\}\)
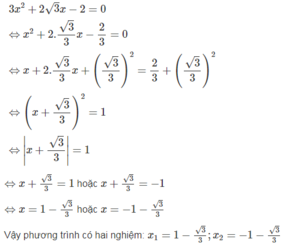
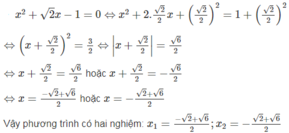
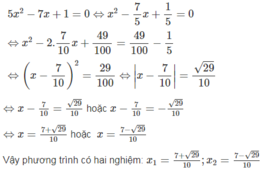
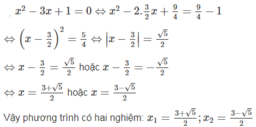
Ta có : 3 x 2 – 6x + 5 = 0 ⇔ x 2 - 2x + 5/3 = 0
⇔ x 2 – 2x + 5/3 + 1 = 1 ⇔ x 2 – 2x + 1 = 1 - 5/3
⇔ x - 1 2 = -2/3
Ta thấy x - 1 2 ≥ 0 và -2/3 < 0
Vậy phương trình vô nghiệm.