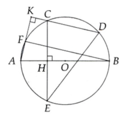
Cho đường tròn tâm O.Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB,nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng: Hai cung nhỏ CF và BD bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 2 2021
a) Xét (O) có: AB đường kính (gt), F ϵ (O)
⇒ △ BAF vuông tại F.
⇒ BF vuông góc với AF tại F. hay BF vuông góc với KF
Mà CD vuông góc với KF tại K (gt)
⇒ CD//BF
⇒ 2 cung nhỏ CF và BD chắn 2 dây // của (O) sẽ bằng nhau.
⇒ Đcpcm
b) Ta thấy CDBF là hình thang cân ( CD//BF, CF = BD )
⇒ 2 đường chéo BC = DF. (1)
Mà △ BCE cân tại B ( vì có BH vừa là đ/c, vừa là đường trung tuyến của △)
⇒BC=BE.(2)
Từ (1) và (2) ⇒ DF = BE.
⇒ cung DF = cung BE
Cộng 2 vế trên với cung EF ta đc:
cung DE = cung BF
⇒ DE = BF
CM
7 tháng 6 2019
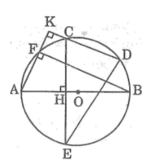
a, HS tự chứng minh
b, Từ giả thiết ta có AB là đường trung trực của CE => B C ⏜ = B E ⏜ = B F ⏜ = D E ⏜
c, Sử dụng mối liên hệ cung và dây
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2023
a.
\(DH\perp AB\left(gt\right)\Rightarrow\widehat{DHB}=90^0\Rightarrow D;H;B\) cùng thuộc đường tròn đường kính DB
\(\widehat{AEB}=90^0\) (góc nội tiếp chắn nửa đường tròn (O)) \(\Rightarrow\widehat{DEB}=90^0\)
\(\Rightarrow D;E;B\) cùng thuộc đường tròn đường kính DB
\(\Rightarrow\) Tứ giác BHDE nội tiếp đường tròn đường kính DB
b.
\(\widehat{ACB}=90^0\) (góc nội tiếp chắn nửa đường tròn (O))
\(\Rightarrow\widehat{ACH}=\widehat{ABC}\) (cùng phụ \(\widehat{BAC}\))
Mà \(\widehat{ABC}=\widehat{AEC}\) (cùng chắn cung AC của (O)
\(\Rightarrow\widehat{ACH}=\widehat{AEC}\)
Xét hai tam giác ADC và ACE có: \(\left\{{}\begin{matrix}\widehat{ACH}=\widehat{AEC}\left(cmt\right)\\\widehat{CAD}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta ADC\sim\Delta ACE\left(g.g\right)\Rightarrow\dfrac{AD}{AC}=\dfrac{CD}{EC}\Rightarrow AD.EC=CD.AC\)
c.
Cũng theo cmt \(\Delta ADC\sim\Delta ACE\Rightarrow\dfrac{AC}{AE}=\dfrac{AD}{AC}\Rightarrow AD.AE=AC^2\)
Áp dụng hệ thức lượng trong tam giác vuông ABC với đường cao CH:
\(BC^2=BH.BA\)
\(\Rightarrow AD.AE+BH.BA=AC^2+BC^2=AB^2=2022^2\)
10 tháng 5 2023
a: góc AEB=1/2*180=90 dộ
góc DHB+góc DEB=180 độ
=>DHBE nội tiếp
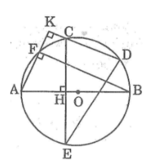
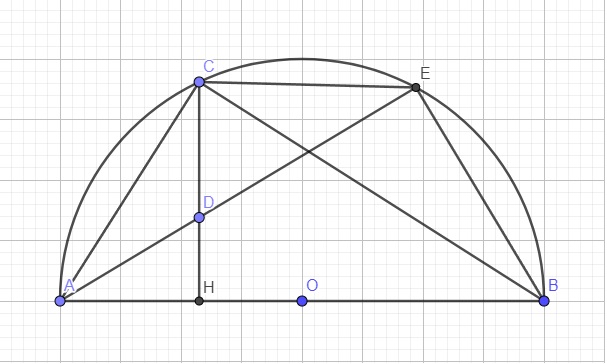
Ta có : ∆ ABF nội tiếp trong (O) và AB là đường kính cuả (O) nên ΔABF vuông tại F
Suy ra: BF ⊥ AK
Mà AK ⊥ CD (gt)
Nên : BF // CD
Suy ra: ∠ BD = ∠ CF
(hai cung bị chắn giữa hai dây song song thì bằng nhau)