A/ SỐ HỌC1. Các cách viết một tập hợp; quan hệ giữa phần tử và tập hợp; các kí hiệu ∈, ∉.2. Phân biệt tập hợp N và N*; thứ tự trong tập hợp N.3. Số phần tử của tập hợp, cách tính số phần từ của tập hợp; khái niệm tập hợp con, kí hiệu ⊂.4. Các phép tính cộng, trừ, nhân, chia (chia hết và có dư) trong N và các tính chất của các phép tính đó; cách tính lũy thừa, nhân, chia hai...
Đọc tiếp
A/ SỐ HỌC
1. Các cách viết một tập hợp; quan hệ giữa phần tử và tập hợp; các kí hiệu ∈, ∉.
2. Phân biệt tập hợp N và N*; thứ tự trong tập hợp N.
3. Số phần tử của tập hợp, cách tính số phần từ của tập hợp; khái niệm tập hợp con, kí hiệu ⊂.
4. Các phép tính cộng, trừ, nhân, chia (chia hết và có dư) trong N và các tính chất của các phép tính đó; cách tính lũy thừa, nhân, chia hai lũy thừa cùng cơ số.
5. Thứ tự thực hiện các phép tính.
6. Các tính chất chia hết của một tổng (hiệu).
7. Các dấu hiệu chia hết cho 2, 5, 3, 9.
8. Khái niệm, cách tìm ước và bội của một số.
9. Khái niệm, cách chứng minh số nguyên tố, hợp số.
10. Cách phân tích một số ra thừa số nguyên tố.
11. Khái niệm, cách tìm ƯC, BC, ƯCLN, BCNN.
12. Khái niệm, cách tìm giao của hai tập hợp
B/ HÌNH HỌC
1. Cách vẽ, cách đặt tên điểm, đường thẳng; quan hệ giữa điểm và đường thẳng; các kí hiệu ∈, ∉.
2. Khái niệm, cách vẽ ba điểm thẳng hàng, ba điểm không thẳng hàng; điểm nằm giữa hai điểm.
3. Cách vẽ đường thẳng đi qua hai điểm, nhận xét.
4. Khái niệm, cách vẽ tia, hai tia đối nhau, hai tia trùng nhau.
5. Khái niệm, cách vẽ đoạn thẳng.
6. Tính chất khi nào thì AM+MB=AB.
7. Cách vẽ đoạn thẳng trên tia, tính chất liên quan đến điểm nằm giữa hai điểm trên tia.
8. Khái niệm, cách vẽ trung điểm của đoạn thẳng.
.
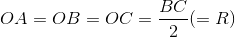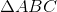vuông tại A.
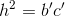ta có: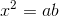 
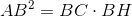ta được 
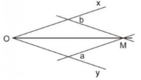
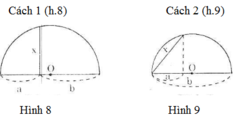
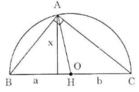
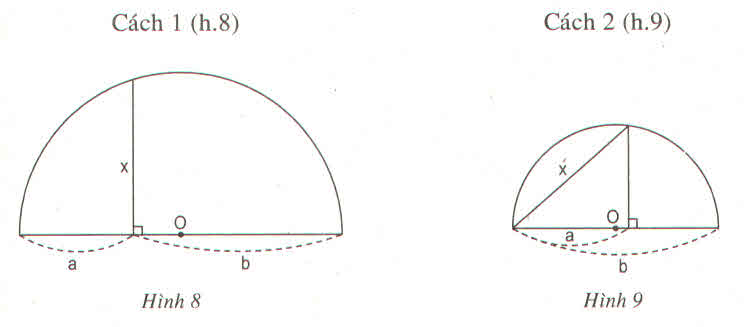
- Cách 1: (h.8)
Theo cách dựng, ΔABC có đường trung tuyến AO bằng một nửa cạnh BC, do đó ΔABC vuông tại D.
Vì vậy AH2 = BH.CH hay x2 = ab
Đây chính là hệ thức (2) hay cách vẽ trên là đúng.
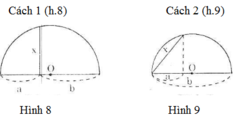
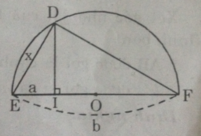
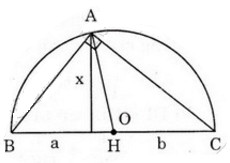
- Cách 2: (h.9)
Theo cách dựng, ΔDEF có đường trung tuyến DO bằng một nửa cạnh EF, do đó ΔDEF vuông tại D.
Vậy DE2 = EI.EF hay x2 = a.b
Đây chính là hệ thức (1) hay cách vẽ trên là đúng.